Artificial Intelligence and Machine Learning
Quantum Many-Body Dynamics from Neural Networks with GPU Acceleration
Principal Investigator:
Prof. Dr. Markus Heyl
Affiliation:
Universität Augsburg, Institut für Physik, Augsburg, Germany
Local Project ID:
qudyngpu
HPC Platform used:
JUWELS Booster
Date published:
Abstract
Experimental advancements within the last two decades have enabled unprecedented control of quantum systems, posing outstanding challenges for their theoretical description. Our project is based on a novel computational strategy at the intersection of machine learning and quantum physics, utilizing artificial neural networks to efficiently represent quantum wave functions. By leveraging supercomputing resources from FZ Jülich and the Gauss Centre for Supercomputing, we have advanced the theoretical understanding of strongly interacting systems in two dimensions, including the first demonstration of the quantum Kibble-Zurek mechanism. Our approach, which is well-suited for distributed computing and GPU-accelerated evaluations, offers an accurate and versatile solution to simulating complex quantum many-body dynamics.
Main Report
Due to the tremendous experimental progress over the past two decades it has become possible today to precisely control quantum systems and to observe their dynamics with unprecedented precision. Motivated by these advancements also the theoretical exploration of such dynamical quantum matter has reached a new level while, however, facing still outstanding challenges. In order to theoretically describe accurately such dynamics in particular for strongly interacting systems it is of key importance to develop of novel computational strategies. This is key to both further develop our theoretical understanding and to establish the crucial link between experimental observations and theoretical descriptions.
In our project, we are pursuing a novel approach operating at the interface between machine learning and quantum physics yielding a powerful theoretical method to solve the complex quantum many-body problem. This approach is based on making use of the impressive capabilities of artificial neural networks, which have been already extremely successful in the context of computer science. Here, these networks are used in the context of quantum physics in order to encode efficiently the fundamental object in quantum physics – the quantum wave function, which contains the full information about the state of a quantum system. The key challenge in quantum physics is that this quantum wave function is itself a high-dimensional object impossible to exactly represent by conventional means on a classical computer when operating in the regime of many particles. Actually, the storage requirements on a classical computer grow exponentially with their number, so that at most a few tens of particles can be captured by exact means. With the so-called neural quantum states approach [1], such high-dimensional objects are written into artificial neural networks, which are particularly powerful for such tasks.
It is our goal to utilize this idea in order to advance the theoretical description of dynamical quantum matter. We focus on a regime, which is particularly challenging for conventional methods in quantum theory: the dynamics of strongly interacting systems in two spatial dimensions. Any progress in this direction within the neural quantum states approach requires extensive GPU resources due to the underlying machine learning structure. Equipped with the supercomputing resources of FZ Jülich and the Gauss Centre for Supercomputing we have been able to further develop this method and, in particular to investigate a series of fundamental physical phenomena in quantum physics. This includes for instance the first theoretical demonstration of the quantum Kibble-Zurek mechanism in two-dimensional systems [2], which is a paradigmatic dynamical phenomenon predicted to display universal behavior when a quantum many-body system crosses dynamically a quantum phase transition – a phase transition that can only occur in quantum systems at zero temperature. An exact theoretical verification, however, has so far been outstanding, which we have been able to achieve for the first time [2].
For our work, access to modern supercomputers is essential. Compared to alternative methods for simulating quantum many-particle systems, our machine learning-inspired approach distinguishes itself by being able to utilize the capacities of supercomputers on a large scale. At its core lies a Monte Carlo algorithm that lends itself well to distributed computing across many nodes of a computer. The most computationally intensive task is the evaluation of neural networks, which can be executed efficiently on GPUs provided by the Jülich Supercomputing Centre.
References
[1] G. Carleo and M. Troyer, Solving the quantum many-body problem with artificial neural networks, Science 355, 602 (2017)
[2] M. Schmitt, M. Rams, J. Dziarmaga, M. Heyl, W. H. Zurek, Quantum phase transition dynamics in the two-dimensional transverse-field Ising model, Science Advances 8, eabl6850 (2022).
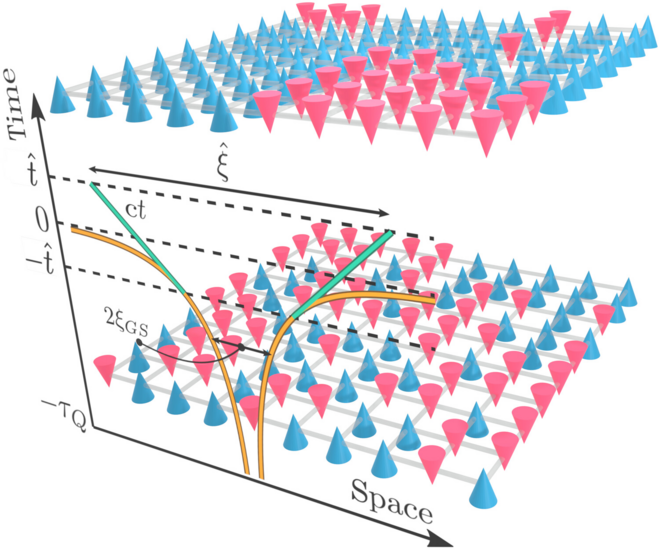
Figure: Illustration of the dynamics across the quantum phase transition in the two-dimensional quantum Ising model. An initially paramagnetic state (bottom), characterized by random orientation of quantum spins, is over time tuned into a ferromagnetic phase (top) characterized by large domains of equally oriented spins. Image taken from Ref. [2].