ASTROPHYSICS
The World’s Largest Supersonic, Magnetohydrodynamic Turbulence Simulation
Principal Investigator:
James R. Beattie and Prof. Christoph Federrath
Affiliation:
Research School of Astronomy and Astrophysics, Australian National University
Local Project ID:
pn73fi
HPC Platform used:
SuperMUC at LRZ
Date published:
Introduction
Supersonic, magnetised turbulence is ubiquitous in the interstellar medium of galaxies. Unlike incompressible turbulence, supersonic turbulence is not scale-free. The scale that marks the transition from supersonic to subsonic turbulence is the so-called sonic scale, which in the context of star formation may define the critical value for which regions inside of molecular gas clouds collapse under their own gravity to form stars. The sonic scale was recently measured for the first time within a hydrodynamical supersonic turbulence simulation using a grid resolution of 10,0483 in [1]. This is the only calculation with sufficient resolution to separate the energy injection scale, supersonic cascade, sonic scale, subsonic cascade and dissipation scale of the turbulence. Whilst this calculation brought great insight into the exact position of the sonic scale and the nature of supersonic turbulence, the influence that magnetic fields have on the sonic scale is more or less unknown, yet is of tantamount importance for understanding the nature of supersonic, magnetized turbulence in the interstellar medium of galaxies.
In this LRZ project, we run the first supersonic, magnetised turbulence simulation that is sufficiently resolved to measure the exact position of the (magneto)-sonic scale, and the supersonic and subsonic energy cascades, to determine how magnetic fields affect the turbulence. We do this by running a magnetohydrodynamical (MHD) turbulence simulation with 10,0803 grid cells, distributed over almost 140,000 compute cores and run for over 60 million compute-core hours on SuperMUC-NG.
Results and Methods
Numerical and high-performance computing methods
We use a modified version of the MHD code flash [2]. Our code uses a highly-optimised, hybrid-precision, second-order, positivity-preserving MUSCL-Hancock HLL5R Riemann scheme [3] to solve the ideal, isothermal, compressible magnetohydrodynamic equations in three dimensions with stochastic, large-scale forcing to drive finite time-correlated supersonic turbulence.
We use a block-structured parallelization, with each 3D computational block distributed onto one single compute core. Each block contains 168x210x210 computational cells, which we pass to each of the 138,240 compute cores (2880 compute nodes on SuperMUC-NG) to give a total grid resolution of 10,0803 grid cells in each of the three dimensions, and 3.0PB of data products in total. To ensure numerical convergence of the plasma statistics, such as the turbulent energy spectra, we also perform simulations at 1,1523 , 2,5203 and 5,0403 grid resolutions.
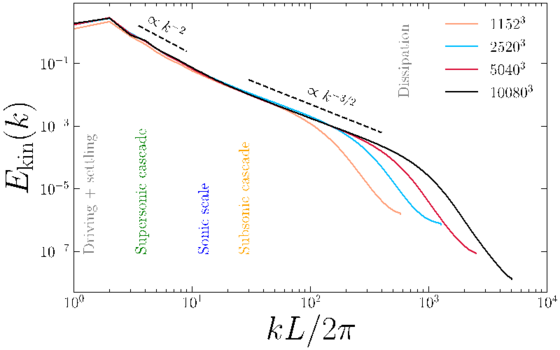
Figure 1. The kinetic energy spectra for compressible MHD turbulence, as a function of wavenumber in units of the box-scale, L/2π , at different resolutions. We show that in the supersonic cascade, Ekink (k)∝k -2 , and in the subsonic cascade, Ekink(k)∝k -3/2 .
Preliminary Results
In Figure 1 we show the kinetic turbulent energy spectra, Ekin(k), where k=2π/l is the wavenumber, at the four different resolutions as indicated by the line colour. The different regimes of turbulence are shown by the background colour, with the magneto-sonic transition traced in blue.
We see two distinct regimes of turbulence emerging in the high-resolution simulations. On small k (large spatial scales, coloured green) the turbulence is dominated by networks of interacting shocks, and has an energy spectrum consistent with Burgers turbulence, Ekin(k)∝k -2 . On large k (small spatial scales, coloured yellow) the energy cascade resembles the incompressible magnetised turbulence Iroshnikov-Kraichnan spectrum, Ekin(k)∝k -3/2 , corresponding to magnetised vortices, which exchange energy and cascade the energy to smaller and smaller spatial scales.
In Figure 2 we show a two-dimensional slice of the three-dimensional gas density in the simulation, revealing strong, shocked gas (coloured red to orange for the most extreme) and deep rarefactions (coloured blue and green for the most under-dense), typical of supersonic turbulence in the interstellar medium. The local magnetic field is shown with a line integral convolution filter, highlighting the intricate, complex, small-scale structure of the field.

Figure 2. A two-dimensional slice of the three-dimensional gas density (red-orange for over-densities, green-blue for under-densities), with three levels of magnification, showing the detailed structures and scales resolved in the 10,0803 MHD turbulence simulation. The local magnetic field direction is visualised with a line integral convolution filter (indicated with grey swirls), showcasing the detailed, small-scale structure of the magnetic field.
Ongoing Research / Outlook
We are currently evolving the 10,0803 simulation further on SuperMUC-NG to produce robust measurements of the turbulence on, above, and below the magneto-sonic scale, across multiple correlation times of the turbulent forcing.
References and Links
[1] C. Federrath et al., Nature Astronomy, 5 (2021) 365-371.
[2] Fryxell et al., Astrophysical Journal Supplement, 131 (2009) 273-334.
[3] Waagan, Federrath & Klingenberg, Journal of Computational Physics, 230 (2011) 3331-3351