ENGINEERING AND CFD

Introduction

The physical process of a laminar boundary layer becoming turbulent is called “laminar-turbulent transition”. Since the flow physics and in particular the skin friction responsible for the drag is significantly influenced by the state of the flow, that is laminar or turbulent, transition plays an important role in external aerodynamics. For example, for rotorcraft computations it was shown that the skin friction was significantly overpredicted (depending on the geometry and the flow state) applying a fully turbulent simulation compared to a simulation that considered laminar-turbulent transition [1]. An overestimation of skin friction leads to an overestimation of power demand which needs to be avoided. However, on complex industrially relevant configurations, like a helicopter rotor, incorporating transition prediction capabilities into the simulation is not straightforward.

State-of-the-art streamline-based methods require a great implementation effort, massive user input and a detailed expert knowledge. Additionally, computing helicopter rotors is inherently computationally expensive, requiring unsteady computations on a fine grid (Fig. 1), with a long computation time to establish the flow. The addition of boundary layer transition to the computation requires even finer time-steps and additional effort to compute the transition position.

Results and Methods 

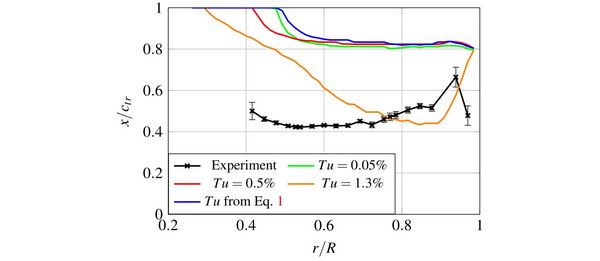
In this project extensive investigations of different approaches to transition modelling on rotors were undertaken, including comparison to experimental data and results of other European CFD codes, see [2]. One finding was that for flows at Reynolds numbers below 500,000 the transition transport models predict unphysically large areas of laminar flow compared to the experimental data, see Fig. 2. To solve this problem a new boundary-layer transition model was developed by Ströer et al. [3,4] to improve the transition prediction for a wide range of parameters crucial to external aerodynamics. The new model was already validated for fixed-wing applications [3,4], and can be used for both compressible and incompressible flows.

A drawback of the model proposed in Refs. [3,4] is the lack of Galilean invariance (GI). For problems where the velocities can be transformed relative to an adjacent wall, the lack of Galilean invariance can be mitigated. However, for complex test cases (like helicopter computations) the formulation of a model should be as universal as possible. Therefore, a new model is under development that is Galilean invariant [5].

The final transition modeling framework [3,4,5] includes a four, a three, and a one equation model. The objective is to provide a flexible framework that can be used to meet rapidly changing industrial requirements. The new models were implemented into the DLR TAU code.

TAU is the compressible finite-volume Navier-Stokes solver of the German Aerospace Center (DLR) used for all computations mentioned. The new model works on either structured or unstructured grids. The simulations performed are RANS computations using an eddy-viscosity type turbulence model for the turbulent flow region.

Fig. 3 shows results for the RTG helicopter rotor. The 2D airfoil was extracted at a constant radial position following Weiss et al. [6]. The figure shows the transition onset position for different collective pitching angles. The agreement of the proposed model with the experimental data is significantly improved compared to the results of the basic transition transport model (γRe_θ model).