ENGINEERING AND CFD
Large-Eddy-Simulations of the Unsteady Aerodynamics of Oscillating Airfoils at Moderately High Reynolds Numbers
Principal Investigator:
Dan S. Henningson
Affiliation:
KTH Royal Institute of Technology, Stockholm (Sweden)
Local Project ID:
PP16163965
HPC Platform used:
Hazel Hen of HLRS and Beskow of PDC KTH
Date published:
Recently there has been a large push in the aircraft industry to reduce its carbon footprint. Laminar flow control and Natural Laminar Flow (NLF) wing design have been proposed as one of the main options for reducing the drag on the airplane and hence its fuel consumption. One of the important aspects of aircraft design concerns dynamic stability and an understanding of the unsteady behavior of NLF airfoils is important for predicting the stability characteristics of the aircraft. Recent experimental studies on NLF airfoils have shown that their dynamic behavior differs from that of turbulent airfoils and that classical linearized models for unsteady airfoils fail to predict the unsteady behavior of NLF airfoils. Most notably, NLF airfoils exhibit non-linear aerodynamic responses to small-amplitude pitch oscillations whereas the classical theories predict only a linear response. In the current work we investigate the dynamics of pitching airfoils to understand the flow phenomenon which causes the breakdown of classical models, and also attempt to describe a new simplified model which takes into account the non-linearities observed in the NLF airfoils.
Introduction
Dynamic stability is an important concern for aircraft designers and the occurrence of an aeroelastic instability in mid-flight can have catastrophic consequences. For the prediction of such an instability early in the design process, simplified mathematical models are used which were laid down in the early 1930s in the works of [1], [2] etc. However, the effects of air transport on climate and global warming have forced the aerospace industry to consider alternate airfoil designs, called Natural Laminar Flow (NLF) airfoils, which have the potential to reduce the fuel consumption of commercial aircrafts and thereby lower the carbon footprint of the industry.
Recent experimental results at DLR [3] and KTH [4] have shown that the classical unsteady models for the prediction of dynamic stability are no longer valid for these NLF airfoils. This failure of the classical models has been traced to the point of transition on the airfoil where flow changes state from laminar to turbulent. The flow state affects the point at which the flow separates from the airfoil which in turn affects the point of transition itself. Thus, these two boundary layer characteristics – point of transition and point of separation - are coupled and lead to new dynamic behavior in unsteady cases which is not modeled by the classical theories.
In this work we study the dynamic coupling between these boundary layer characteristics for unsteady airfoils with the aim to create an improved mathematical model to predict the aeroelastic stability characteristics of airfoils.
Methodology and Results
The dynamics of flow around airfoils depends on the Reynolds number (Re) which is a parameter defining the ratio of the largest to the smallest spatial scales in the flow. Commercial aircrafts fly at Reynolds numbers of the order of 106-107. On the other hand, aeroelastic instabilities typically exhibit long time scales. Computationally this becomes challenging since a large range of spatial scales must be simulated to get accurate predictions of boundary layer transition and separation, and the simulation must also evolve over long time scales for the relevant aeroelastic instabilities. In our work we numerically simulate a pitching wing at a Reynolds number of 750,000 which is very close to the Reynolds number range of high-altitude long-endurance aircraft. A high-order Spectral-Element Method code Nek5000 is used for the numerical simulation [5] and 1.4 x 109 grid points were necessary to discretize the problem.
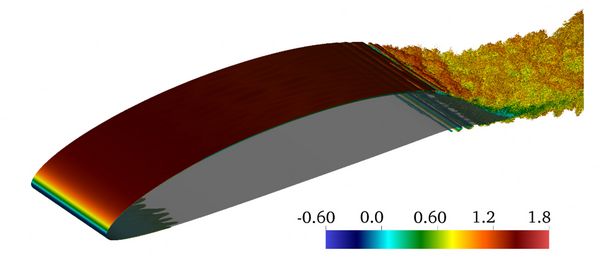
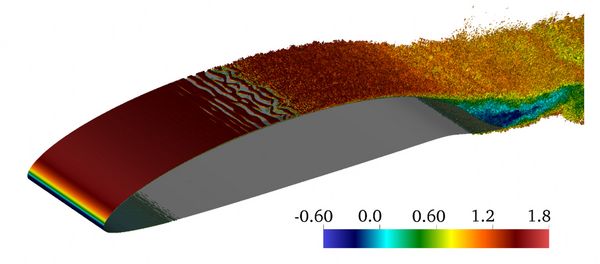
The time varying boundary layer transition and separation is tracked throughout the simulation. Figure 1 and Figure 2 show the instantaneous flow states at the minimum and maximum angles of attack.
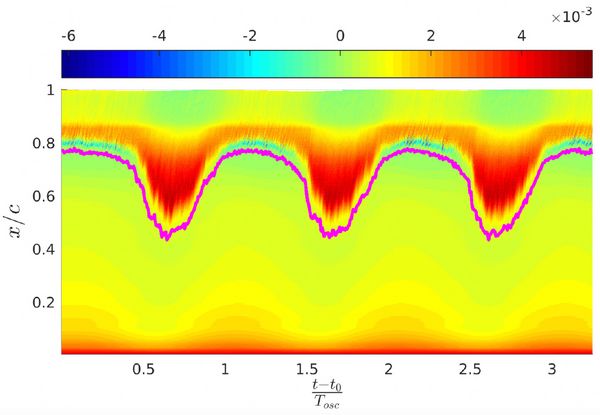
Figure 3 shows the space-time variation of the shear stress on the top of the wing, along with the time varying transition point (pink line). This variation in transition point produces the non-linear aerodynamic response. Despite large separated regions, the transition point movement has a regular repeating upstream-downstream motion in each cycle.
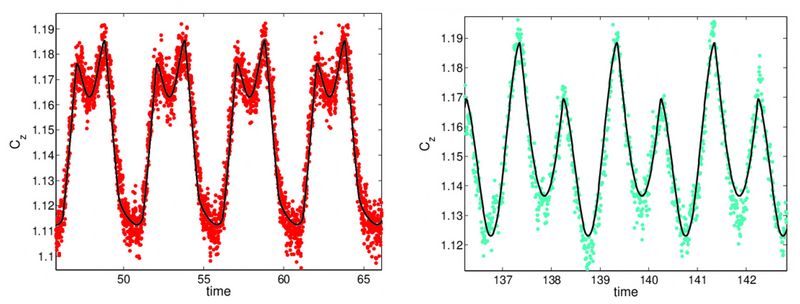
The simulation results have shown that the non-linear aerodynamic response can be modeled using a simple (three parameter) empirical model. Figure 4 shows the unsteady normal force on the airfoil for two different cases. The lines indicate the results of the empirical model with points indicating the experimental data. A good agreement has been found between the data and the model for a wide range of frequencies. The model connects the flow around stationary airfoils to the behavior of flow around unsteady pitching airfoils [6] which suggests that results could be generalized to different airfoils.
The results obtained so far suggest that it may be possible to model and predict the non-linear aerodynamic response using computationally inexpensive tools. Such tools benefit aircraft designers since the design process requires parametric studies and access to computationally inexpensive tools is essential for such parametric design analysis. Furthermore, aeroelastic instabilities may be predicted with a high confidence level much earlier in the design process, thus reducing substantially the cost of experimental tests for stability analysis.
Outlook and Future work
Several subsequent analyses are in progress with the data generated from the simulations. The simplified model for aerodynamic forces so far is empirical and work is under way to create a predictive model so that a-priori stability analysis can be performed. In addition, linear growth of small disturbances in the flow in such unsteady wing cases has hitherto not been investigated. Changes in the growth of small disturbances dictate the unsteady transition point on the airfoil. Furthermore, the changes in turbulence subject to unsteady modulation is not well understood and is one of the aspects that will be investigated in the current work.
Project Team
Prabal Negi, Ricardo Vinuesa, Philipp Schlatter, Ardeshir Hanifi and Dan S. Henningson
References
[1] H. Glauert, "The force and moment on an oscillating aerofoil," in Vorträge aus dem Gebiete der Aerodynamik und verwandter Gebiete: Aachen 1929, A. Gilles, L. Hopf and T. Kármán, Eds., Berlin, Heidelberg: Springer Berlin Heidelberg, 1930, pp. 88-95.
[2] T. Theodorsen, "General theory of aerodynamic instability and the mechanism of flutter," 1935.
[3] H. Mai and A. Hebler, "Aeroelasticity of a laminar wing," in Proceedings IFASD, Paris, 2011.
[4] M. Lokatt, "On Aerodynamic and Aeroelastic Modeling for Aircraft Design," 2017.
[5] P. F. Fischer, J. W. Lottes and S. G. Kerkemeier, "Nek5000 Web page," 2008. [Online]. Available: http://nek5000.mcs.anl.gov.
[6] P. Negi, A. Hanifi and D. Henningson, "LES of the Unsteady Response of a Natural Laminar Flow Airfoil," in 2018 Applied Aerodynamics Conference.
Scientific Contact:
Prof. Dan S. Henningson
Department of Mechanics
KTH Royal Institute of Technology
Stockholm, Sweden 100 44
e-mail: henning [@] mech.kth.se
NOTE: This project was made possible by PRACE (Partnership for Advanced Computing in Europe) allocating a computing time grant on GCS HPC system Hazel Hen of the High Performancee Computing Center Stuttgart (HLRS).
HLRS project ID: PP16163965
July 2019