ENGINEERING AND CFD
Statistical and Geometrical Properties of Turbulent Flows with Viscosity Stratification
Principal Investigator:
Michael Gauding
Affiliation:
Université de Rouen, Rouen (France)
Local Project ID:
hfg00
HPC Platform used:
JUQUEEN of JSC
Date published:
The turbulent motion of fluid flows is a complex, strongly non-linear, multi-scale phenomenon, which poses some of the most difficult and fundamental problems in classical physics. Real turbulent flows encountered in engineering and environmental applications are very often characterized by a spatial or temporal variation of its thermo-physical properties, like viscosity or density. A prominent example from geophysical flows is the convection in the earth's mantle, where the viscosity and density decreases with temperature. An other important case is the turbulent mixing in combustion systems, where a concentration dependent viscosity may affect the efficiency of turbulent mixing. A better understanding of these phenomena leads to a better modelling of turbulent mixing and, for example, an improved prediction of the pollutant formation in combustion engines.
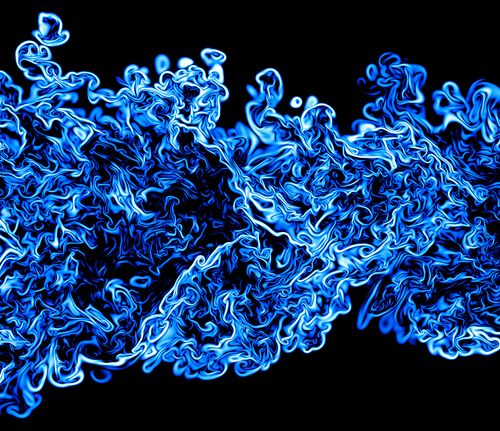
Fig. 1: Slice through the field of the scalar dissipation reveals the small-scale structure of turbulence.
Copyright: CNRS UMR 6614 CORIA and JSCViscosity represents the most important property of turbulent flows, and the impact of its variation on the dynamics should be addressed in detail. According to Kolmogorov's first hypothesis, the smallest scales of turbulent flows should reveal universal properties, and should depend only on two parameters, namely the viscosity and the mean energy dissipation rate. However, the dissipation is a highly fluctuating quantity with large but rare excursions from its mean value. In the literature this phenomenon is called internal intermittency. The physical mechanism behind internal intermittency is still unresolved, and it is not known whether viscosity gradients enhance or reduce internal intermittency. Figure 1 shows the field of the scalar dissipation which is characterized by very fine filamented structures.
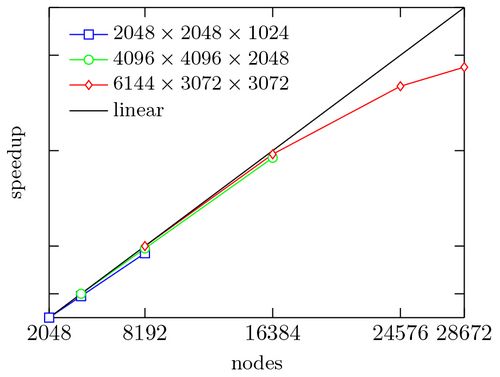
Turbulent flows reveal a tremendous number of degrees of freedom, which makes numerical approaches very challenging. A well-established numerical technique to treat the "turbulence problem" is the so-called direct numerical simulation. Direct numerical simulation (DNS) solves the governing equation for all relevant time and length scales without relying on any turbulence models, and hence provides highly resolved three dimensional fields of all quantities of interest. Due to the steadily increasing capabilities of supercomputers, DNS has become an indispensable tool in the field of turbulence research. Within the present project the researchers performed DNS of turbulent shear flows with up to 231 billion grid points. The high-resolution DNS provides novel insight into the physical mechanism behind the small-scale motion of turbulent flows. The flow solver psOpen has been developed to efficiently carry out simulations of this size on supercomputers. psOpen uses a hybrid parallelization approach and non-blocking communication techniques to overlap communications and computations. In 2015, psOpen became member of the HighQ-Club at Jülich Supercomputing Centre. Figure 2 shows the scaling of psOpen up to 2 million threads on the supercomputer JUQUEEN.
Fig. 2: The DNS solver psOpen exhibits a nearly ideal strong scaling up to the full machine for the largest case.
Copyright: CNRS UMR 6614 CORIA and JSCThe principal question that is addressed by the present project is the self-similarity of turbulent flows with variable viscosity. The concept of self-similarity has played an important role in shaping the understanding of turbulent flows. Several problems in turbulence have been approached by self-preservation or self-similarity hypotheses imposing restrictions on the dynamics of the flow. By a combination of theoretical techniques and highly resolved direct numerical simulations, the scientists found two new main results. Firstly, the self-preservation of a turbulent flow is broken by fluctuations of the viscosity, while secondly, the mean dissipation becomes independent of fluctuations of the viscosity (which confirms Taylor's postulate).
From a statistical analysis it was further shown that turbulent flows with variable viscosity are characterized by an enhanced level of small-scale intermittency, which results in the presence of smaller length scales and a modified turbulent mixing.
References:
M. Gauding, J. H. Goebbert, C. Hasse and N. Peters, Line Segments in Homogeneous Scalar Turbulence, Physics of Fluids 27, 9, 095102, 2015
J. H. Goebbert, M. Gauding, Direct Numerical Simulations of Fluid Turbulence at Extreme Scale with psOpen, Technical Report of the JUQUEEN Extreme Scaling Workshop, 2015
F. Hunger, M. Gauding, C. Hasse, On the impact of the turbulent/non-turbulent interface on differential diffusion in a turbulent jet flow. Journal of Fluid Mechanics, 10;802:R5, 2016
J. H. Goebbert, M. Gauding, C. Ansorge, B. Hentschel, T. Kuhlen, H. Pitsch, Direct Numerical Simulation of Fluid Turbulence at Extreme Scale with psOpen, Proceedings of the International Conference on Parallel Computing, 2016
N. Peters, J. Boschung, M. Gauding, J.H. Goebbert, R.J. Hill, H. Pitsch, Higher-order dissipation in the theory of homogeneous isotropic turbulence. Journal of Fluid Mechanics, 803:250-74, 2016
M. Gauding, L. Danaila, E. Varea, High-order structure functions for passive scalar with mean gradient, International Journal of Heat and Fluid Flow, 2017
M. Gauding, L. Danaila, E. Varea, Dissipative range statistics of turbulent flows with variable viscosity, Proceedings of the 10th International Symposium on Turbulence and Shear Flow Phenomena, 2017
Scientific Contact:
Michael Gauding
CNRS UMR 6614 - CORIA
Université de Rouen
Saint Etienne Du Rouvray, France
michael.gauding [at] coria.fr
Jens Henrik Goebbert
Institute for Advanced Simulation (IAS)
Jülich Supercomputing Centre (JSC)
Forschungszentrum Jülich, Germany
j.goebbert [at] fz-juelich.de
JSC project ID: hfg00
May 2017