ELEMENTARY PARTICLE PHYSICS
Disconnected Contributions to Generalized Form Factors (GPDs)
Principal Investigator:
Andreas Schäfer
Affiliation:
Institute for Theoretical Physics, Regensburg University (Germany)
Local Project ID:
pr74po, pr48gi, pr84qe
HPC Platform used:
SuperMUC of LRZ
Date published:
The main focus of high energy physics research is the search for signals of physics beyond the Standard Model. Many of the experiments built for this purpose involve protons or neutrons (collectively termed nucleons), either in the beam, such as at the Large Hadron Collider at CERN, or within the nuclei of the targets, such as those used for dark matter detection experiments. In order to extract information on the underlying interactions occurring in these experiments between quarks and other fundamental particles, one needs to know the distribution of the quarks within the nucleon. Lattice QCD simulations of the strong interactions between quarks and gluons can provide information on the momentum, spin and angular momentum of these particles within the nucleon. In general one distinguishes between elastic scattering processes where the nucleon is left intact and inelastic scattering where the nucleon is destroyed. Both aspects can be parameterized in terms of quark and gluon generalized parton distributions (GPDs). These will be measured at the proposed Electron Ion Collider (EIC) in the US. This project computes the moments of the GPDs, the so called generalised form factors. Disconnected contributions must be evaluated in order to access the moments for the individual quark flavours.
Introduction
Modern particle accelerators, like the LHC at CERN, Switzerland, or the planned EIC (Electron Ion Collider) in the US, are distinguishable by their extremely high luminosities, i.e. extremely high collision rates, and thus extremely large statistics. The reason why this is so important, e.g. at LHC, is that the “Standard Model” has proven to be so successful that possible signals for “New Physics” tend to be very small and thus require such large statistics to be observable. However, this development also implies that the Standard Model predictions have to become ever more precise. In fact, not to waste any discovery potential of these accelerators, the precision of the relevant theoretical Standard Model calculations should always be better than what is reached experimentally. As the present degree of accuracy is already very high, this becomes an ever more difficult requirement to fulfill, especially for the needed lattice QCD input because QCD is the most difficult part of the Standard Model and calculating the non-perturbative structure of hadrons is the most challenging task of QCD. Also for lattice simulations the control of systematic errors thus became the crucial requirement which has to be met. Let us add that QCD itself is well established and tested beyond any reasonable doubt, so the question is not whether QCD describes hadron physics (we know that it does) but to reach such a level of precision that even small deviations from Standard Model predictions can be established with high reliability.
All of this applies in particular to the structure of protons and nuclei as these are collided at the LHC and EIC. While in earlier times experiments were basically only sensitive to the spin and momentum fraction of the interacting quarks and/or gluons, by now various correlations became relevant. These can be correlations between quarks which affect so called Multi-Parton-Interactions at LHC which are one of the dominating sources of systematic uncertainty, or correlations between quark polarization and its transverse (with respect to the collison axes) position or momentum within a proton or quark-gluon correlations which enter as so-called higher-twist contributions and many more. As a consequence, all of these contributions have been classified systematically within the framework of perturbative QCD and Operator Product Expansion such that one knows in principle which quantities should be calculated on the lattice. However, these quantities are so many and are so varied and complicated that lattice QCD faces a truly challenging task. Most probably, the physically motivated demands can only be met by ever larger and resource-full collaborations, like CLS. Of the systematic uncertainties of lattice simulations the most important one is the continuum extrapolation. The symmetries of the real, continuum theory differ from those of the discretized one, defined on a hypercubic lattice and are only regained in the limit of vanishing lattice spacing. For the Wilson fermion action chiral symmetry, which is one of the most relevant symmetries of low-energy QCD is, e.g., only regained in the continuum limit. Because the physical volume needed for a reliable lattice simulation is kept, reducing the lattice spacing by a factor implies an increase in required lattice points by the fourth power of this factor. Therefore, controlling the continuum limit is the most demanding task. In addition it becomes ever more difficult to achieve ergodicity of the functional integrals to be calculated with Monte-Carlo methods with respect to the topologically distinct sectors of QCD when the lattice spacing is reduced.
We are part of an international collaboration of collaboration named CLS (Coordinated Lattice Simulations) which aims at reaching the required precision and control of systematic errors in particular with respect to the continuum limit. A large number of quark and gluon field ensembles was generated by CLS with a variety of quark masses and lattice spacings chosen such as to minimize the total systematic uncertainties. To avoid the problem of topological freezing, alluded to above, novel, open boundary conditions were used, see figure 1.

Figure 1: Some of the ensembles generated by the CLS collaboration and used for the projects reported on. Every dot stands for one or several ensembles (with different physical volumes) of typical more than a thousand field configuration generated for the plotted lattice spacing “a” and pion mass, which depends on the chosen light quark masses. The physical pion has a mass of roughly 135 MeV. One has to extrapolate the results to the physical point marked in red. Two additional groups of ensembles were generated.Green dots symbolise ensembles the production of which is finished. Yellow dots mark ensembles for which generation is ongoing.
Copyright: University of RegensburgFigure 1 needs some additional explanation: The numerical cost of lattice simulations depends strongly on the masses assumed for the light quarks, i.e. the up and down quark. At the same time effective field theories allow to extrapolate quite reliably in the quark masses. This extrapolation is most efficient if ensembles exist both for constant sum of up- down- and strange quark mass but varying individual quark masses (figure 1) and for physical strange quark mass and varying up- and down quark masses (the second set of ensembles, which is not shown). The third set of ensembles is generated for symmetric quark masses and is needed to determine the non-perturbative (i.e. all order) renormalization factors with high precision. By performing a combined fit to all ensembles one obtains the optimal result for continuum extrapolated and renormalized observables at physical quark masses. Obviously this whole program requires a major effort, but the needed resources are still small compared to those invested in the experiments.
One specific aspect which is also crucial to reduce the total systematic uncertainties is the inclusion of the so called “disconnected contributions” which were often neglected in older lattice calculations, an approximation which can no longer be justified. Their evaluation is at the center of the projects on which we report. The strange quark content of the proton is, e.g., described by disconnected contributions. Note that recent ATLAS data from LHC have established that it is much less understood than previously assumed, see figure 2. While this discrepancy is most obvious at very small momentum fraction, which is not directly accessible in lattice simulations the situation is different for the longitudinally polarized strange quark distribution Δs(x), see figure 7.
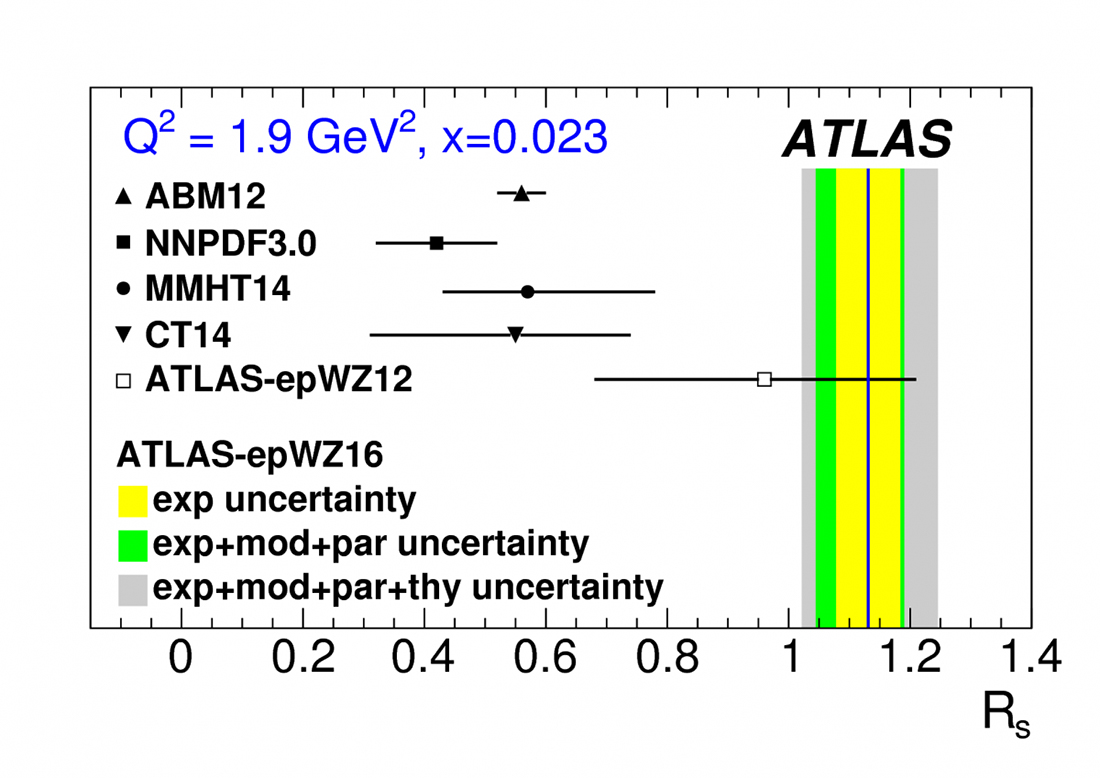
Figure 3: Recent result from the Atlas collaboration at the LHC [1]. Rs is the ratio of the strange and light quark sea (i.e. the amount of quark-antiquark quantum fluctuations). Due to the much larger strange quark mass this was for decades assumed to be substantially smaller than unity (see black dots representing the “knowledge” prior to these new data). The different colored bands represent different statistical and systematical uncertainties.
Copyright: University of RegensburgResults and Methods
Our strategy (and that of CLS in general) as sketched in the Introduction can be illustrated by comparison with results by the European Twisted Mass Collaboration [2] which recently published results for several of the quantities we calculate based on just one ensemble generated on an exceptionally coarse lattice and small physical volume. Obviously, with just one lattice spacing the continuum limit cannot be taken and thus no reliable systematic uncertainty can be given. In return, however, ETMC generated a large ensemble at physical quark masses which allowed to obtain statistically precise results for several of the phenomenologically most discussed quantities and thus has had a substantial impact on the ongoing physics discussion. In contrast, our strategy, which controls all systematic uncertainties, is far more time consuming. We produce global fits to all of our ensembles and compare in an automated manner hundreds or even thousands of different fits and extrapolations to obtain realistic systematic uncertainties. This requires much more manpower wall-clock time. (Also, we calculate many more quantities in parallel than what was done in [2] to profit from strong synergies.) Presently, all the needed 3-point functions have been calculated, which was the objective of our LRZ-proposals, but the task of analysing these (which requires much less compute power) is still ongoing. Therefore, let us illustrate the adopted procedure with results of an earlier analysis of the connected parts of moments of Generalized Parton Distributions (GPDs) of the nucleon. GPDs contain a lot of detailed information on hadron structure as is illustrated in figures 4 and 5, which show some of our lattice results for so-called tensor GPDs (nucleons are described by eight leading-twist GPDs.). Obviously, the spin directions and quark positions are strongly correlated in a nucleon, resulting in asymmetries which could be misinterpreted as signals for new physics if these correlations would not be known from the lattice. Figure 8 shows a distribution of the values obtained for very many different fits and extrapolations for certain GPD matrix elements each of which describes a different physical correlation. The resulting half-maximum width is cited as systematic uncertainty. The results are for physical quark masses.

Figure 4 (left): Probability distribution of down quarks in a proton moving towards the observer (i.e. in the positive z direction). The center of longitudianl momentum of all quarks and gluons defines the origin in the x-y plane. Left: The proton spin points in the positive x direction, the quark spin is not observed. Right: The quark spin points in the positive x direction, the proton spin is not observed. -- Figure 5 (right): Same as figure 4 but for the up quark.
Copyright: University of RegensburgHaving discussed the role of the continuum extrapolation in such detail, it is somewhat surprising that our results for those ensembles already analysed agree quite well with those of [2] as is illustrated in figure 6 and 7, in which we show the spin carried by the strange quarks and antiquarks in a proton and the spin carried by the light quarks. All forms of angular momentum of quarks and gluons (spins and orbital angular momenta) have to add up to the total proton spin of one half, but the size of the individual contributions was hotly debated for many years. In these figures the black diamonds are our new results while the blue crosses are results from our earlier calculation [3]. The green symbols represent the results from [2] while the NNPDF crosses indicate phenomenological fits to experiment. The dashed vertical line indicates the physical pion mass to which all results at larger mass have to be extrapolated, as well as to vanishing lattice spacing. If the continuum limit would really be as benign as suggested by this agreement, this would be great news for our prospects of ultimately reaching the required precision in lattice simulations.
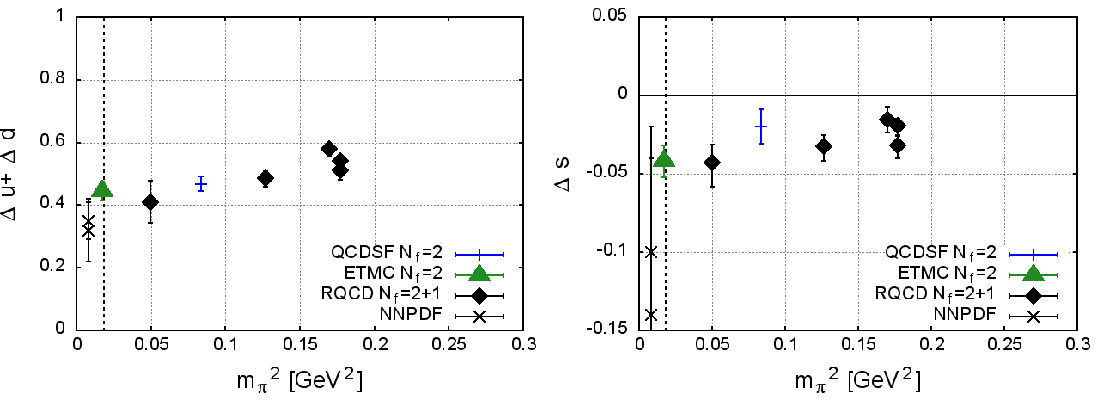
Figure 6 (left): Comparison of our new result (black diamonds) our old results [3] (blue symbols) the results of [2] and empirical fits. The upshot is that all results are in good agreement with one another. -- Figure 7 (right): Same as figure 6 but for the spin carried by the strange quarks and antiquarks.
Copyright: University of RegensburgAnother one of the many aspects of state of the art lattice simulations is the non-perturbative renormalization mentioned above. Radiative corrections differ for a discretized lattice QCD action and the continuum QCD action and thus an a relative, finite renormalization step is required. The needed corrections to be applied to lattice results are typically of order 10-20 percent and obviously have to be known rather precisely to reach an over all percent precision. This is possible using sophisticated numerical procedures but requires substantial computer time. We have simulated a substantial number of additional ensembles and have carefully optimized our algorithmic procedures to determine the renormalization factors with high precision.
Codes Used
In line with our remarks about the synergies and large scale collaborations required to meet the demands of present day particle physics, we use open source code going under the name of CHROMA [4]. We also will make the CLS configurations public available on the ILDG (International Lattice Data Grid). For the first bunch of ensembles this will happen as soon as some technical problem at the ILDG host site is resolved. To overcome the problem of topological freezing we developed tools to simulate with open temporal boundary conditions instead of periodic or antiperiodic ones. Their advantage is that topological charge can enter or leave the lattice volume and their disadvantage that the lattice volume close to the edges cannot be used due to artifacts, resulting in a loss of up to 30 percent of the useable volume. For these simulations the open source software package openQCD was developed. The main numerical task in lattice simulations is the inversion of the Clover-Wilson Dirac operator, which is an very large sparse matrix on the lattice. The numerical inversion cost grows drastically when the light quark masses are reduced to their physical values. Therefore, various state-of-the-art techniques have to be used, e.g., domain decomposition and deflation. The latter uses the property of local coherence of the lowest eigenmodes to effectively remove them from the operator which results in a greatly improved condition number and a cheaper and cost efficient inversion. For the generation of the gauge ensembles within the CLS effort.
There are many other features that make this software very efficient, including twisted-mass Hasenbusch frequency splitting that allows for a nested hierarchical integration of the molecular dynamics at different time scales, decoupling the quickly changing but cheaper forces of the action from the more expensive low frequency part of the fermion determinant.
Within the interdisciplinary SFB/TRR-55 “Hadron physics from lattice QCD” we closely collaborate with collegues in Applied Mathematics at Wuppertal University who are experts in the required taks. This resulted in much superior matrix inversion algorithms, like an adaptive, aggregation based multigrid solver which we have not only extensively used but also made publically available within CHROMA.
Not surprisingly, by substantially increasing the performance of our codes we ran into the Big Data problem of handling the very large ensembles generated by CLS as well as the very many correlators we analyse.
This requires us to use libraries that support parallel IO. The Hierarchical Data Format (HDF5) is by now our standard format and greatly simplies the management of big amounts of data. Using Data-Grid technology established by the experimental groups at the LHC we are also able to move such large files in short times. (In fact, by making available the technology and know-how computer centers contribute signicantly to the success of large-scale efforts like the CLS one.)
Research Team
G. Bali, V. Braun, S. Bürger, S. Collins, B. Gläßle, M. Göckeler, M. Gruber, F. Hutzler, M. Löffler, B. Musch, S. Piemonte, R. Rödl, D. Richtmann, E. Scholz, J. Simeth, W. Söldner, A. Sternbeck, S.Weishäupl, P. Wein, T. Wurm, C. Zimmermann
References
1] M. Aaboud et al. [ATLAS Collaboration],Eur. Phys. J. C 77 (2017) 367; arXiv:1612.03016
[2] C.Alexandrou et al. Phys. Rev. Lett. 119 (2017) 142002; arXiv:1706.02973.
[3] G.S.Bali et al. Phys.Rev.Lett. 108 (2012) 222001; arXiv:1112.3354.
[4] R.G.Edwards et al. [SciDAC, LHPC and UKQCD Collaborations], Nucl. Phys. Proc. Suppl. 140 (2005) 832; hep-lat/0409003.
Scientific Contact:
Prof. Dr. Andreas Schäfer
Institut für Theoretische Physik, Universitaet Regensburg
D-93040 Regensburg/Germany
andreas.schaefer [@] physik.uni-r.de
NOTE: This report was first published in the book "High Performance Computing in Science and Engineering – Garching/Munich 2018":
LRZ project ID: pr74po
January 2019

