ELEMENTARY PARTICLE PHYSICS

The simulation of nuclear matter at nonzero baryon density presents a notoriously hard problem in lattice QCD. The usual simulation strategies depend on the exploration of the configuration space by interpreting the weight of each configuration in an average as a probability, which is however not valid here as the weight is non positive. This is called the ‘sign problem’ of nonzero density QCD. In this project, the researchers use a method based on the Complex Langevin equation evading the sign problem to map out the phase diagram of nuclear matter.

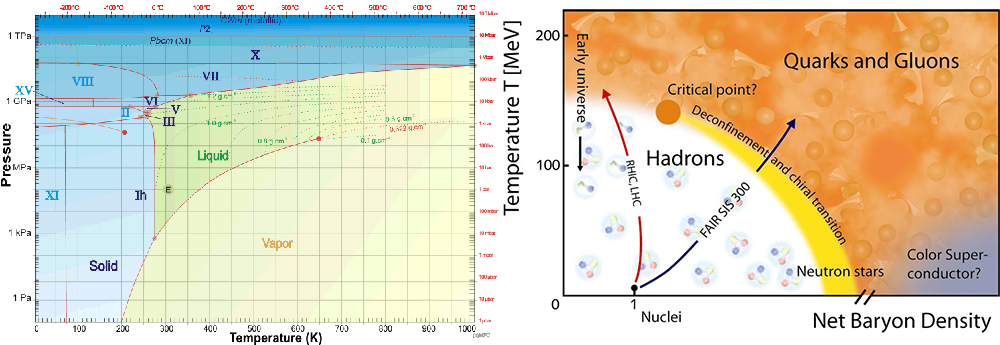
The different phases of water (liquid water, vapour and ice) are well known to everybody, and almost everyone knows even the temperature at which the water changes its phase i.e. it gets frozen or boils to vapour. Systematic studies yield the phase diagram of the water as a function of the temperature and the pressure, well known to both experimental and theoretical physics.

The behavior of quarks and gluons, which make up the nuclei of atoms is governed by the theory called Quantum Chromo Dynamics (QCD). This theory describes how quarks build up protons, neutrons and other particles at low temperatures (with the help of an attractive force mediated by gluons), and the quark-gluon plasma at high temperatures. One of the current outstanding problems of theoretical physics is to produce a phase diagram for QCD as a function of the temperature and the baryonic density.

Currently very little is known about the phase diagram of QCD, but effective models give some guidelines as illustrated above. The simulation of nuclear matter and quark gluon plasma at small baryon densities has been a well established part of theoretical physics for decades. In lattice QCD, the quarks and gluons are placed on a space-time lattice where they can move around and interact. Their behavior on this lattice is governed by relatively simple equations, however the solution of the equations typically requires the use of supercomputers.

There are very sophisticated algorithms based on the so called ‘importance sampling’ which uses the fact that the system can be described with an ensemble of configurations describing an instance of gluon and quark fields. Each configuration has a weight which is interpreted as a probability depending on the temperature, quark masses and so on. This probabilistic description, however, breaks down as soon as there is a nonzero baryonic density in the system, because the weight of each configuration can now become negative. This is the infamous ‘sign problem’, a long standing challenge in the field of lattice QCD as well as other fields such as condensed matter physics, non-equilibrium physics, etc.

The researches use a simulation method based on the so called Langevin equation which describes a random walk in configuration space and can be used as a simulation method also at zero densities. This method, however, does not require the interpretation of weights as probabilities, and therefore is generalizable to non-positive weights as well. This generalization is based on the structure of the complex numbers, hence it has the name ‘Complex Langevin equation (CLE)’ . It was invented more than 30 years ago [1], however its status was unclear as sometimes this method gives unreliable results. In recent years, however, important results have clarified which conditions must be satisfied and which technical improvements are needed to make the method and its results trustworthy [2,3].

Here, the researchers have determined the phase diagram of “Heavy Dense QCD” [4], an approximation to the real world QCD, where it is assumed that the quarks are so heavy that they don't move. In this approximation the sign problem is still present, but additional numerical problems connected to light quarks do not appear. In Fig. 2, the phase diagram is shown, characterized by the density which shows whether there are more quarks than anti-quarks on the lattice, and the “Polyakov loop” which shows whether the quarks are confined to hadronic particles like proton, neutron, pion, etc. or can move freely on their own. Note that there is some resemblance to the proposed phase diagram of QCD on Fig.1., though quantitative agreement as well as the richness of the QCD phase diagram is not to be expected here as in this system the quarks are very heavy.

The results of this project help to estabilish the CLE method as a possible way to solve the real world QCD eventually, as well as providing benchmark values for various other methods proposed to try to evade the sign problem of QCD.