ELEMENTARY PARTICLE PHYSICS
Impact of Magnetic Fields on Dense Strongly Interacting Matter
Principal Investigator:
Dr. Bastian Brandt
Affiliation:
Universität Bielefeld, Fakultät für Physik, Bielefeld, Germany
Local Project ID:
pn36ri
HPC Platform used:
SuperMUC-NG PH1-CPU at LRZ
Date published:
Introduction
The strong interactions as part of the Standard Model of particle physics are described by Quantum Chromo-dynamics (QCD). Due to its strong coupling at typical energy scales in today’s Universe, predictions for strongly interacting matter, such as the one of the quark-gluon plasma, appearing in collisions of heavy nuclei at the Relativistic Heavy Ion Collider (RHIC) and future efforts, cannot be obtained using perturbative methods. The numerical treatment of QCD, discretized on a spacetime lattice – lattice QCD – has proven to be a viable tool to investigate the properties of QCD in the strongly coupled regime. Due to the strong coupling, quarks and gluons are confined into hadrons at low energies, while asymptotic freedom implies the existence of a phase with quasi-free quarks and gluons at high energies, i.e., high temperatures or quark densities, for instance. The phase transition between these two phases is the subject of intense theoretical and experimental research and also of particular interest for astrophysics and cosmology.
For simulations in lattice QCD, the regime at non-zero baryon density remains inaccessible due to the complex action problem and can only be accessed indirectly through extrapolations from vanishing or imaginary chemical potentials. In particular, this also concerns the possible existence of a critical endpoint, separating the crossover line of the QCD transition from a hypothetical first order phase transition at large chemical potentials. In recent years, several different extrapolation schemes have been explored [1, 2], showing agreement with direct simulations at small volumes.
Apart from a non-zero baryon density, a broad range of physical systems also feature strong magnetic fields, such as magnetars, off-central heavy-ion collisions and, potentially, even the early Universe. For a phenomenological description of such systems, incorporating the effects due to the magnetic field – an external field on typical QCD timescales – is mandatory, but a systematic study is still missing. The properties of QCD subject to an external magnetic field at vanishing quark densities are by now well understood, including the strengthening of the crossover and the existence of a critical endpoint in the phase diagram. Naturally the question arises whether the two critical endpoints (if both exist) are connected by a single critical line. Consequently, studying the impact of the combination of magnetic fields and quark densities on the equation of state and the phase structure is important not only for the description of the aforementioned physical systems, but also might provide a different angle on one of the long-standing questions concerning the phase diagram at vanishing magnetic field.
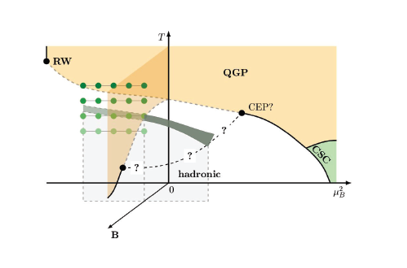
Figure 1: Conjectured QCD phase diagram in the space of temperature, chemical potential and magnetic field.
Results and Methods
In our study we are investigating the properties of QCD subject to both non-zero chemical potential and external magnetic fields using Taylor expansion and analytic continuation from imaginary chemical potentials. In this first step, our main interest is in the equation of state (EoS) in the phenomenologically relevant setup for heavy-ion collisions where the freeze-out conditions are met. The conditions are: 1) a fixed ratio between the baryonic density and the charged-particle density con-straint given by the number of valence quarks present in the colliding ions; 2) the strangeness neutrality, due to the absence of valence strange quarks in the ions. These conditions can be implemented by tuning charge and strangeness chemical potentials when changing the baryon chemical potential. The tuning coefficients can be related to chemical potential susceptibilities [3], which we computed from our simulations at vanishing chemical potential. In the initial stage of the project, we obtained, for the first time in the literature, the proportionality coefficients, between these chemical potentials, labelled q1 and s1 for the charge and strangeness chemical potentials, respectively, as a function of temperature for different magnetic field strengths [4]. As an example, we show the s1 coefficient, ensuring strangeness-neutrality in Figure 2. For this success the usage of SuperMUC-NG has been essential, since a large number of gauge field configurations for 30 different ensembles with sizeable lattices (8×323) had to be generated for each value of the magnetic field. In addition, the computation of the observables is numerically expensive, due to large numbers of random vectors necessary to evaluate the operator traces accurately. For an efficient use of SuperMUC-NG our code has been specifically optimized for such large scale cluster architectures.
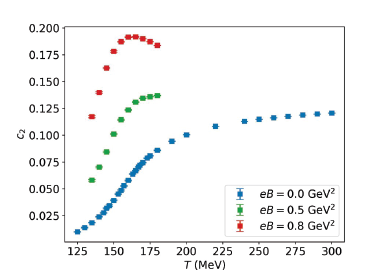
Figure 2: Coefficient between the strangeness and baryon chemical potential that ensures strangeness-neutrality in our simulations.
In terms of physics, the results from Figure 2 can be understood by the suppression of the hadronic contributions of protons and lambda-baryons to the partition function due to the presence of the magnetic field. This leads to a decrease of q1 and an increase for s1, respectively.
Using the tuning coefficients, we were able to compute the leading-order Taylor coefficient for the extrapolation of the Equation of State (labeled c2) to real and imaginary chemical potentials for the three different magnetic field values as functions of temperature. The results are shown in Figure 3. Even these preliminary results can be used to benchmark future heavy-ion collision models that take into account both finite densities and magnetic fields.
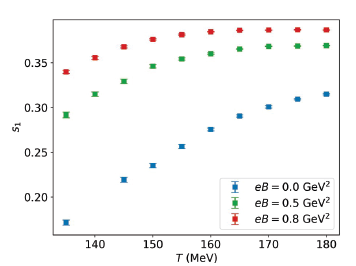
Figure 3: Leading-order Taylor coefficient of the Equation of State as a function of temperature for three values of the magnetic field.
Ongoing Research / Outlook
Currently we work on the fine tuning of charge and strangeness chemical potentials to match the experimental setup of heavy-ion collisions, in order to start the first simulations at non-zero imaginary chemical potentials. Those are needed for the final and precise extrapolation to real chemical potentials. In this process the explicit isospin breaking and the strangeness neutrality conditions have to be taken into account, which are expected to lead to further deviations from the tuning at vanishing magnetic field [5]. Eventually, the calculation of high-order fluctuations at imaginary chemical potentials will for the first time lead to an accurate calculation of the EoS for the phenomenologically relevant heavy-ion setup, discussed above, featuring finite baryon density and non-zero magnetic fields.
References and Links
[1] S. Borsányi, J.N. Günther, R. Kara, Z. Fodor, P. Parotto, A. Pásztor, C, Ratti, and K. K. Szabó, Phys. Rev. D, 105, no.11 (2022), 114504, 2022.
[2] S. Borsányi, Z. Fodor, J. N. Guenther, R. Kara, S. D. Katz, P. Parotto, A. Pásztor, C. Ratti, and K. K. Szabó, Phys. Rev. Lett., 126 (2021), 232001.
[3] A. Bazavov et al., Phys. Rev. Lett. 109 (2012) 192302.
[4] S. Borsányi, B. B. Brandt, G. Endrödi, J. Guenther, R. Kara, and Valois, A. D. M. QCD. 12 2023.
[5] S. Borsányi et. al. Phys. Rev. Lett. 125 (2020) 052001.