ELEMENTARY PARTICLE PHYSICS
Matter Anti-Matter Annihilation in Charmonium
Principal Investigator:
Prof. Dr. Francesco Knechtli
Affiliation:
Bergische Universität Wuppertal
Local Project ID:
pn29se
HPC Platform used:
SuperMUC-NG at LRZ
Date published:
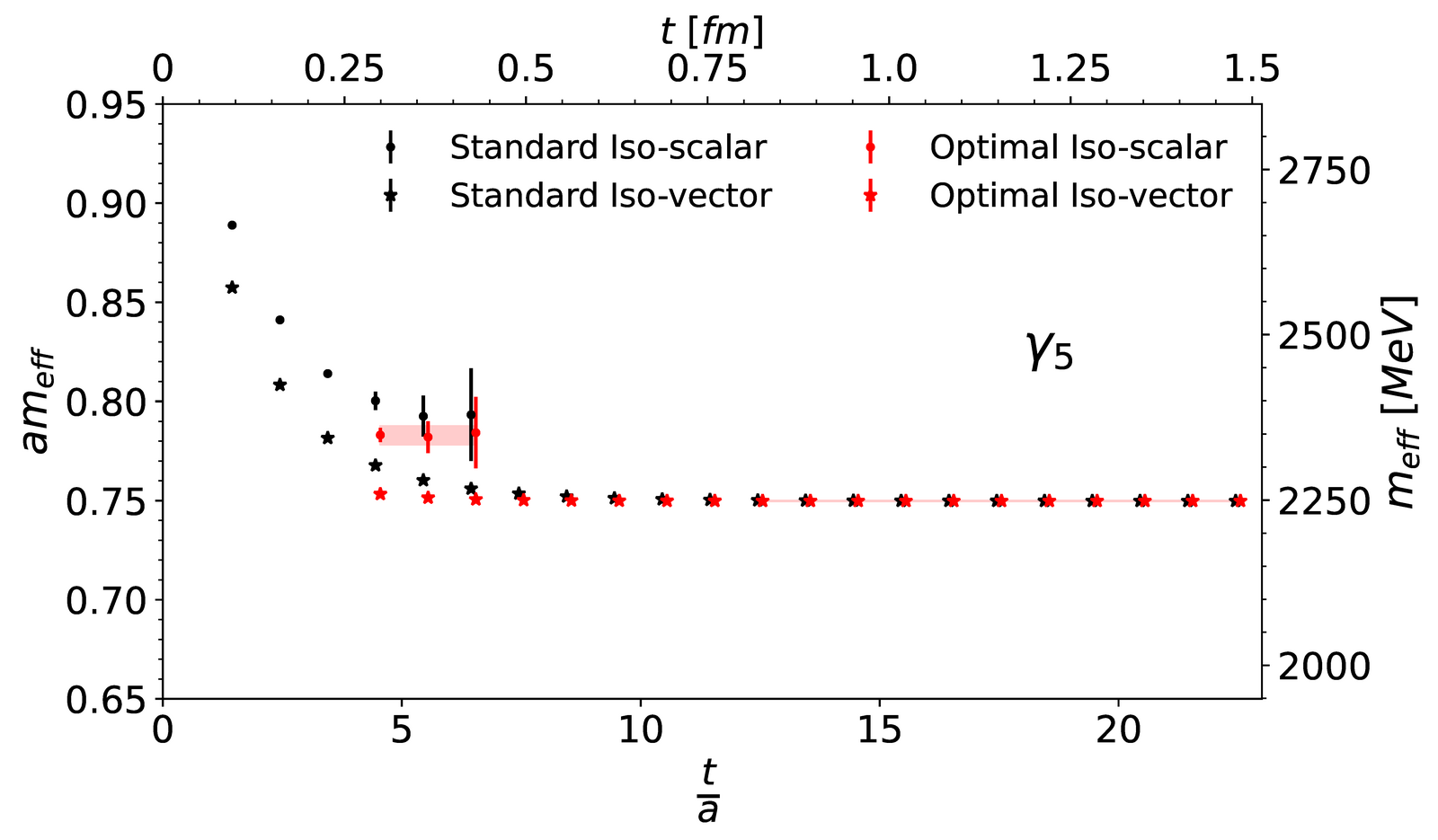
Figure 1: Effective masses of the pseudoscalar meson ηc. Comparison of the iso-scalar and iso-vector mesons. The iso-scalar meson includes the effects of charm-annihilation.
Introduction
Quantum Chromodynamics (QCD) is the sector of the standard model describing the strong nuclear force, which binds quarks and gluons inside hadrons. The theory confines these constituents, which are never observed directly in experiment.
In this project we study charmonium, a system containing a charm quark-anti-quark pair. These studies underwent a revolution after a number of entirely unexpected narrow resonances called the X, Y and Z states were discovered by the Belle and BaBar experiments at the start of the new millennium. In spite of almost two decades of theory investigations, no clear picture of the internal mechanics of these resonances has emerged. Excitations of constituent gluons are likely to be an important part of some candidate hybrid states. Extensive experimental studies of charmonium and the XYZ states are underway at LHCb at CERN and there are significant plans at new experiments such as Belle II at the SuperKEKB B-factory and BESIII at BEPC and a future Super-c-tau factory. Moreover, the PANDA (Anti-Proton ANnihilation in DArmstadt) experiment at FAIR (Facility for Antiproton and Ion Research), GSI in Darmstadt plans a first anti-proton beam in 2025. PANDA will search for exotic states in charmonium and glueballs, which are states made predominantly of gluons.
Lattice QCD provides a framework to study charmonium from first principles. A rich spectrum is seen, including candidate hybrids in recent calculations however these use an approximation where states are assumed to be stable and charm-quark annihilation effects are neglected. The mass of charmonia are extracted from the exponential fall-off of the correlator in the Euclidean time separation between source and sink of the meson. Charm annihilation contributions are quark-line disconnected diagrams where the charm quark and anti-quark annihilate at the source and sink. They constitute the significant remaining uncertainty in precise calculations of the low-lying charmonium states. Charm-annihilation effects are suppressed by the Okubo-Zweig-Iizuka (OZI) rule, but these dynamics are poorly understood. For example, they contribute to a shift in the mass of the pseudoscalar particle, the ηc meson. This shift has the wrong sign in leading order perturbation theory. Charmonium has the same energy scale as the pseudoscalar glueball. The quantum mechanical mixing of charmonium with glueball states occurs through these charm-annihilation diagrams. This mixing affects the validity of the OZI rule beyond perturbation theory and is studied in this project.
The investigations reported here are part of the research programme of project 1 “The confined gluon: precision spectroscopy with charm quarks” in the Research Unit “Future methods for studying confined gluons in QCD” (FOR 5269) [1] funded by the Deutsche Forschungsgemeinschaft (DFG).

Figure 2: Strong scaling of the inversion of the Dirac operator on a lattice of size 96x483. We show the ratio of the run-time the inversion takes on SuperMUC-NG with 768 cores to the run-times it takes using more cores (speedup). The red dashed line is the ideal speedup. In the legend BS means the block size in the deflated SAP GCR solver.
Results and Methods
We have analysed 4,800 gauge configurations of lattice size 48x243 and lattice spacing a=0.066 fm. We employ a technique called distillation [2] which we have improved in this project [3]. The computationally most intensive part of the calculation requires solving the Dirac equation with the right-hand sides given by 200 eigenvectors of the 3D gauge Laplacian on each of the 48 time-slices of the lattice. The number of solutions of the Dirac equations (inversions) per gauge configuration equals 38,400. The quark mass in the Dirac operator corresponds to approximately half of the value for the charm quark in nature.
Figure 1 shows the effective masses of the ground state in the pseudoscalar channel. They plateau for large values of the time separation t/a between source and sink of the meson to the value of the mass of the particle, which in this case corresponds to the ηc meson in nature. The points marked by circles are obtained from the iso-scalar correlator, which includes the contribution of charm-annihilation and the points marked by stars are obtained from the iso-vector correlator, where charm-annihilation is absent. For the data points coloured in red we used our optimised distillation technique. The black data points are obtained with standard distillation and are shown for comparison. It is evident that with the optimal distillation method the effective masses reach their plateau at earlier times than they do with the standard distillation method. This is crucial to determine the mass of the iso-scalar meson. Due to the charm-annihilation effects the statistical errors of the data for the iso-scalar meson increase rapidlly with the time separation t/a. The charm-annihilation effects lead to an upward shift in the iso-scalar meson mass compared to the iso-vector meson mass. We estimate this shift to be 99 MeV with an uncertainty of 15 MeV. In nature this shift has been indirectly estimated to be about 7 MeV. We expect that the number and the mass of the charm quarks in our model calculation, which differ from their values in nature together with the absence of light quarks account for the difference in the mass shift. For the future we plan a calculation in a physical setting.
To achieve this precision, we developed a software package for the measurement of correlation functions using the improved distillation method. Our programs are based on “QCDlib”, a library written by us in C+MPI, that facilitates massively parallel QCD calculations. The inversions of the Dirac operator are performed by calling the package openQCD [4], namely a deflated SAP GCR solver with AVX instructions enabled for SuperMUC-NG. The computations for 4800 gauge configurations of lattice size 48x243 ran on 384 cores (8 nodes) of SuperMUC-NG and required about 17 millions core-hours.
We have applied our method to 16 times larger gauge configurations of lattice size 96x483. The setup is the same as described above but with a smaller lattice spacing a=0.049 fm and using 325 eigenvectors of the 3D Laplacian per time-slice. Figure 2 shows the timings for one inversion of the Dirac operator as a function of the number of cores used on SuperMUC-NG. We plot the ratio of the run-time on 768 cores to the run-times using more cores (speedup). The red dashed line corresponds to the ideal speedup. The performance of our code is close to the ideal line and shows its good scalability. Using different block sizes (BS) corresponds to changing this parameter in the deflated SAP GCR solver used. We have analysed 250 gauge configurations of lattice size 96x483. These computations ran on 6912 cores (144 nodes) and required about 20 millions core-hours. The number of cores 6912 was chosen because, even though we begin to see deviations from the ideal speedup in the inversion times, it allows for more parallelisation in the temporal direction.
Ongoing Research / Outlook
We plan to compute the charmonium spectrum with hybrid candidates and the effects of charm-annihilation on close-to-physical gauge configurations of size 144x483 which include the dynamics of three light degenerate quarks, whose mass is the same as the average light quark mass in nature and a physical charm quark [5]. This will provide information on mass and quark content dependence of the spectrum of charmonium. The Research Unit FOR 5269 [1] will develop new numerical algorithms for calculations of glueballs and charmonium including their mixing and decays. We will also apply some of the new techniques to compute the potential between a static (infinitely massive) quark and anti-quark pair. The latter is a first principle input to effective theories to study the spectrum and decays of charmonium including exotic XYZ candidates.
References and Links
[1] confluence.desy.de/display/for5269
[2] M. Peardon et al. [Hadron Spectrum Collaboration], Phys. Rev. D 80 (2009), 054506.
[3] F. Knechtli, T. Korzec, M. Peardon, J.A. Urrea Niño, arXiv: 2205.11564
[4] luscher.web.cern.ch/luscher/openQCD/
[5] R. Höllwieser, F. Knechtli, T. Korzec [ALPHA Collaboration], Eur. Phys. J. C 80 (2020) no.4, 349
Scientific Contact
Prof. Dr. Francesco Knechtli
Bergische Universität Wuppertal
Fakultät für Mathematik und Naturwissenschaften
Theoretische Teilchenphysik
Gaussstr. 20
D-42119 Wuppertal
+49 202 439 2630
knechtli@physik.uni-wuppertal.de