ELEMENTARY PARTICLE PHYSICS
Numerical Simulations of Continuum Field Theories
Principal Investigator:
Prof. Fakher Assaad
Affiliation:
Institute for Theoretical Physics, Würzburg
Local Project ID:
pr53ju
HPC Platform used:
SuperMUC-NG at LRZ
Date published:

Fig.1 Possible flow diagrams for the SO(5) non-linear sigma model in the stiffness versus symmetry breaking term plane. Our simulations favor quasi-criticality (a) or an SO(5) CFT (b). See https://link.aps.org/doi/10.1103/PhysRevLett.126.045701
Introduction
The defining properties of our numerical research in the domain of correlated electron systems are the notions of emergence and criticality. It is amazing to realize that starting with a collection of interacting electrons, new particles, corresponding to collective excitations, that carry different quantum numbers than the original electron, can emerge. Emergence only occurs in the thermodynamic limit where the volume of the system is taken to infinity at constant particle number. An example is the canonical spin ½-chain realized for example in KCuF3. Here, a spin-flip carrying spin 1 decays into two spinons that are gapless and perceive no confining potential. This state of matter is critical: it has no length scale and allows for a continuum field theory description. From the theoretical point of view, the one-dimensional spin chain can be described in many seemly different ways. On one hand, one can write the spin 1/2 degree of freedom as a fermion bilinear, with the constraint on one electron per site. A Feynman path integral formulation will lead to compact quantum electrodynamics (QED) in 1+1 dimensions. The spin ½-chain actually has a higher symmetry than the spin rotational symmetry. It has an O(4) one, that unifies seemingly different correlation functions: spin-spin and dimer-dimer ones. The continuum field theory that captures this state of matter is the O(4) non-linear sigma model in 1+1 dimensions with a Wess-Zumino-Witten geometrical term. The above provides one of many examples of why continuum field theories are important in the realm of the solid state: they account for universal and emergent behavior at or in the vicinity of critical points. They equally provide a common language between high-energy and solid state physics.
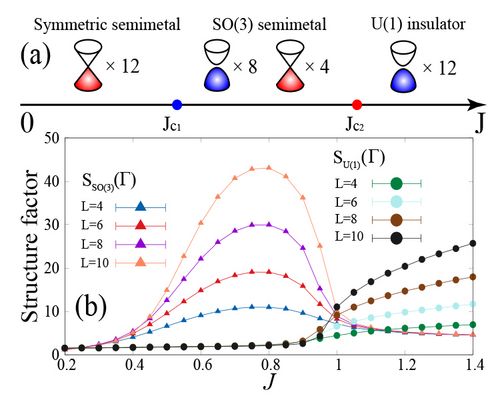
Fig. 2 Reproduced from Ref. [5]
Results and Methods
To investigate collective phenomena in the solid state without any approximations other than system size, we use auxiliary field quantum Monte Carlo (QMC) methods [2]. This approach samples the Feynman path integral formulation of the grand canonical partition function and is hence a method of choice to study systems in thermodynamic equilibrium. In 2017, we started to develop a generic auxiliary field package, Algorithms for Lattice Fermions (ALF) [2] with the help from DFG and KONWIHR funding. During this grant period, we have released version 2.0 of the software [2], and we are continuously developing it. The challenges we confront when simulating fermionic system include a) the sign problem reflecting the fact that the action is generically complex and b) potentially long autocorrelation times. There has been remarkable progress in understanding how to formulate negative sign free simulations for an ever-growing class of problems. In the absence of this problem, the computational cost scales as the third power of the volume,V, times the inverse temperature, β. This scaling and the desire to reach large lattices so as to at best capture critical and emergent phenomena renders the use of supercomputers imperative. Most of the research we have carried out would not have been possible without access SuperMUC-NG. In fact access to substantial CPU time has given us the freedom of starting ambitious research projects that have been published in high-impact journals.
One of the major achievements of this grant proposal was to provide a Landau Level regularization of the O(5) 2+1 dimensional non-linear sigma model with Wess-Zumino-Witten geometrical term [3]. This continuum field theory is the dimensional generalization of the aforementioned O(4) theory in 1+1 dimensions accounting for the physics of the one-dimensional Heisenberg chain. Aside from the intrinsic interest in understanding the phase diagram of this continuum field theory, it is a candidate theory of so called deconfined quantum criticality that unifies two orders (e.g. anti-ferromagnetism and valence bond solid) into a higher symmetry [4]. For this project the challenges were the following. i) To simulate a continuum field theory, one needs to provide a regularization. Here we simulate a 2+1-dimensional Nf=4 two-component Dirac system akin to graphene, supplemented with 5 anti-commuting mass terms. This model has the desired O(5) symmetry, and in the presence of a gap, integrating out the fermions will generate the desired model. A standard lattice regularization is not an option since it would break the O(5) symmetry of the model. On the other hand, using a Landau level regularization, by projecting the model onto the lowest Landau level, will do the job. The number of flux quanta defines the degeneracy of the Landau level and the dimension of the Hilbert space in which we will define the simulation. ii) It is amazing to see that this formulation supports a negative-sign free formulation such that large scale numerical simulations are tractable. iii) Even in the absence of the negative sign problem we were confronted to many difficulties and we refer the interested reader to the supplemental part of our publication [3] for further reading. In short, the projection forces us to work with long-ranged interactions such that the computational cost scales as V5β which is two powers in volume larger than generic simulations with short ranged interactions. Furthermore, the memory cost scales as V3β rather than as V2 β for short-ranged interactions. Our results are summarized in Fig. 1, and supports the idea that this field theory is close to a SO(5) critical phase, such that the flow diagram of Fig. 1 (c) is supported by the data. Clearly the possibility that the two critical points in Fig.1 (c) collide so as to produce the quasi-critical behavior shown in Fig. 1 (a) is also a possible interpretation of our data.
Ongoing Research/Outlook
We have recently introduced models of Dirac fermions that show novel quantum critical behavior [5]. The phase diagram is shown in Fig. 2. Here we consider 12 Nf=2 Dirac cones with an interaction, J, that produces a unique phase diagram. First, at Jc1, we observe a partial gapping out of the Dirac cones. This metallic quantum critical point is novel. We have computed exponents, but they are at odds with those computed with a variety of analytical methods. The reason for this mismatch is intriguing and defines a set of novel questions. Are we suffering from quasi-criticality where system sizes beyond reach are required to capture the critical behavior? Is the continuum field theory, SO (3) Gross-Neveu, put forward to understand this transition misleading?
The second transition is even more interesting since the numerical data supports a continuous transition between different broken symmetry phases. Landau forbidden transition between anti-ferromagnets and valence bond solids have attracted considerable attention. In particular the aforementioned SO (5) field theory seems to capture the quasi-universality of this transition. Our instance of a Landau forbidden transition does not fit into the above theory since it involves gapless Dirac fermions. In short, the model and numerical results obtained in Ref. [5] define a set of tantalizing questions that will impact our future research.
The above summarizes only one aspect of our research where Dirac fermions play an important role. Other topics that we are and will continue investigating are heavy fermion systems, frustrated spin systems, electron-phonon problems as well as various lattice gauge theories.
On the algorithmic front, the ALF code is now rather mature. Since, to the best of our knowledge, it is the only general implementation of the auxiliary field quantum Monte Carlo method, we believe that it will set a standard. Of importance for future developments is: i) ease of use and 2) efficiency on novel supercomputing architectures. Concerning ease of use, we have and are developing a Python interface to the Fortran2003 ALF code. As for efficiency, one of our future goals is to provide a GPU version of the ALF ode, so as explore possible speedups for large lattice.
References and Links
[1] Project pr53ju.
[2] ALF 2.0, Scipost 2022, accepted
[3] Z. Wang et al. Phys. Rev. Lett. 126 (2021), 045701.
[4] Y. Liu at al. Nat. Comm. 10 (2019), no. 1, 2658.
[5] Z. Liu et al. arXiv:2108.06346 (Phys. Rev. Lett. 2022 accepted)
Science Contact
Prof. Dr. Fakher Assaad
Theoretische Physik I
Julius-Maximilians-Universität Würzburg
Am Hubland
97074 Würzburg
Deutschland
E-Mail: assaad@physik.uni-wuerzburg.de