ELEMENTARY PARTICLE PHYSICS
The Δ Resonance in Elastic Nucleon-Pion Scattering
Principal Investigator:
Prof. Dr. Carsten Urbach
Affiliation:
Helmholtz-Institut für Strahlen- und Kernphysik, Universität Bonn, Germany
Local Project ID:
GCS-HSRP
HPC Platform used:
Hawk and HAZELHEN of HLRS
Date published:
Abstract
Collisions of protons and pions are usually observed and measured in particle accelerators. Thanks to today’s powerful supercomputers we can study these elementary particles also in theory, namely based on the core principles of Quantum Chromodynamics. By simulating the fundamental quark and gluon fields on a space-time lattice not only can we investigate why protons (and pions and many other particles) emerge at all from the strong force, but also their reaction with each other, for example in an elastic collision. And sometimes such collisions bring forth entirely new, short-lived particles, like the Δ resonance. Our project is dedicated to applying the Lattice QCD method to track from fundamental quarks and gluons to the Δ particle.
Introduction
The nuclear matter we experience in everyday life is built from protons and neutrons in the core of atoms. These nucleons in turn are composite particles made from the fundamental quarks, and we view them as three quarks bound together by the strong force. In the Quantum world the strong force acting means the exchange of gluons between the quarks. To our present knowledge there are six types (“flavors”) of quarks, namely up, down, charm, strange, top and bottom. Up and down quarks are the ones with lowest mass among them, and most important for the physics we discuss.
To each quark there is an anti-quark, which interacts the same way with the strong force gluons, but has e.g. opposite electric charge. A quark and an anti-quark will bind together to form a meson. The lightest meson is built from an up and an anti-down quark and is called a Pion (π).
So by the strong force hadrons such as Nucleons and Pions emerge from binding the fundamental quarks together, a process known as Hadronization. At this hadronic level, we ask our question: How do Nucleons and Pions interact? A basic reaction is their elastic 2-particle scattering, meaning a collision of a Nucleon with a Pion going in, and equally coming out of the collision. This is one of the fundamental nuclear reactions that we must understand to describe the dynamics e.g. inside the cores of atoms.
When a Proton and a Pion collide in this way, their quarks and anti-quark can rearrange to form a new, intermediary particle state, the Δ resonance, which exists for a certain time, and finally decays again into a Proton and a Pion.
The famous Δ resonance is well-known from scattering experiments. Our fundamental theory for the mechanism of how quarks and gluons interact is Quantum Chromodynamics (QCD). Much easier said than proven: Everything else pertaining to the strong interaction, e.g. the phenomenon of hadronization, many properties of elementary particles such as Protons and Pions, should follow from the basic physics laws of QCD for quarks and gluons.
The goal of our project is to investigate how QCD leads us from the quark-gluon interaction to the features of Nucleon-Pion scattering, and most of all the appearance of the Δ resonance.
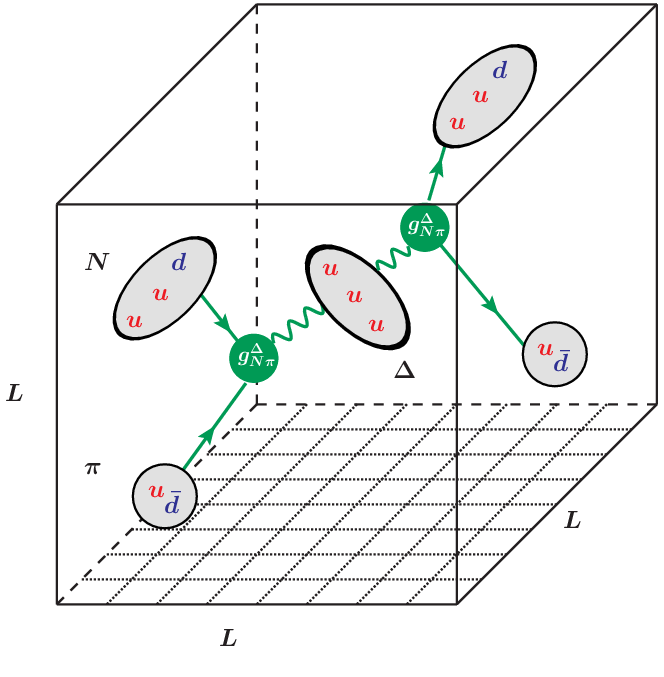
Figure 1: Illustration of the elastic Nucleon-Pion scattering with the quark model: down and anti-down quark initially annihilate and finally recreate during the overlap of Nucleon and Pion, while the three up quarks form a Δ, which propagates until decay.
Results and Methods
Tracking fundamental quark-gluon interaction to Nucleon-Pion scattering means at its core solving the equation of motion for quarks and gluons in Quantum Chromo-dynamics. However, that is not something we can solve as straightforwardly as the equation of motion for an apple falling in earth’s gravitational field.
Instead, we simulate the actions of quarks and gluons based on the very laws of QCD. Our physics stage, on which the simulated quarks and gluons interact, is a cubic box of side length L a few femtometer (10-15m), and they exist for a time length T. Inside the box we discretize space and in time, and so solve QCD on a finite lattice.
These Lattice QCD simulations are powered by High Perfomance Computing on hardware like the former HAZELHEN and presently HAWK Supercomputer at HLRS. These machines provide computational resources that allow our simulations to reach a fine discretization of our lattice and light enough up and down quark, so that we can compare our simulation results directly to experiment.
In practice we simulate the time-evolution on the lattice of Nucleon-Pion 2-particle states. After its excitation the signal for such a lattice state decays exponentially, and from the decay rate we infer the energy of the state.
One numerical core task in constructing this time evolution is the solution of the lattice QCD Dirac equation, which is the equation of motion for the quark field (ψ), in a given background gluon field (A). We illustrate the degrees of freedom on a 2-dimensional plane (with the 4-dimensional space-time lattice) in Figure 2.
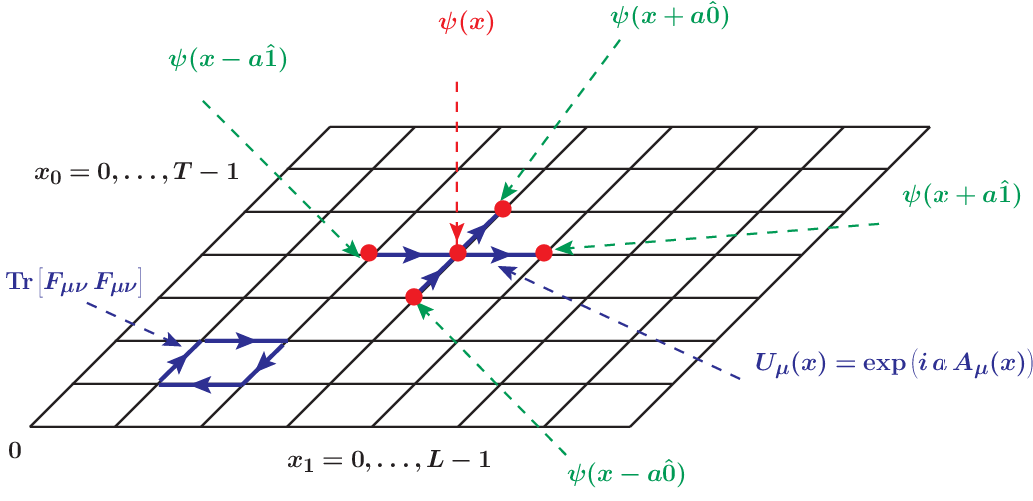
Figure 2: Illustration of fields on the space-time lattice
From these solutions for the quark fields we compute the propagation of the composite Nucleon and Pion fields, which is the second core task. The two tasks are repeated for several hundred samples of gluon field configurations, a process by which we approximately solve also the gluons’ equation of motion.
The finite volume of our simulated lattice enforces a permanent interaction of Nucleon and Pion, they cannot separate sufficiently to not mutually influence each other in the box. This influencing predominantly stems from elastic scattering and was shown by Martin Lüscher to be encoded in a small shift in energies of Nucleon-Pion states when restricted to a box of finite size L.
Thus, from the precise computation of the Nucleon-Pion energy levels we infer information about Nucleon-Pion scattering and the Δ resonance.
The project GCS-HSRP Acid 44113 was the first stage of a longer-lasting effort within the Extended Twisted Mass Collaboration (ETMC) to tackle Nucleon-Pion scattering at physical quark mass. Within this project we laid the ground work for the computational method, which we now apply successfully in follow-up projects. Our first complete analysis has recently been published in Reference [1] and we illustrate our result by the shift in the complex phase between ingoing and out-going Nucleon-Pion state in Figure 3, which displays the typical S-shaped rise across the resonance region. Further details are given in Reference [1].
Ongoing Research/Outlook
The computational techniques developed during GCS-HSRP Acid 44113 are now applied to numerical investigation of other pressing questions in Nucleon-Pion physics. One of these is: How do Nucleon-Pion states influence the coupling of a Nucleon to a Photon or a Neutrino? Initial results have been reported in Reference [3].
Studying the Δ is but the first step in the investigation of Nucleon resonances in Lattice QCD, but even with today’s powerful computing resources a challenging one. With future improvements of methods and algorithms for production of simulation data, as well as computing hardware, controlled calculations of scattering of Nucleon with one or two Pions will come into reach.
References
[1] C. Alexandrou, S. Bacchio, G. Koutsou, T. Leontiou, S. Paul, M. Petschlies and F. Pittler: Phys.Rev.D 109 (2024) 3, 3
[2] C. Alexandrou, S. Bacchio, G. Koutsou, S. Paul, M. Petschlies, F. Pittler: PoS LATTICE2022 (2023) 120
[3] C. Alexandrou, G. Koutsou, Y. Li, M. Petschlies, F. Pittler: talk at XL . International Symposium on Lattice Field Theory, Fermilab 2023, Contribution ID: 159, 2312.15737 [hep-lat]
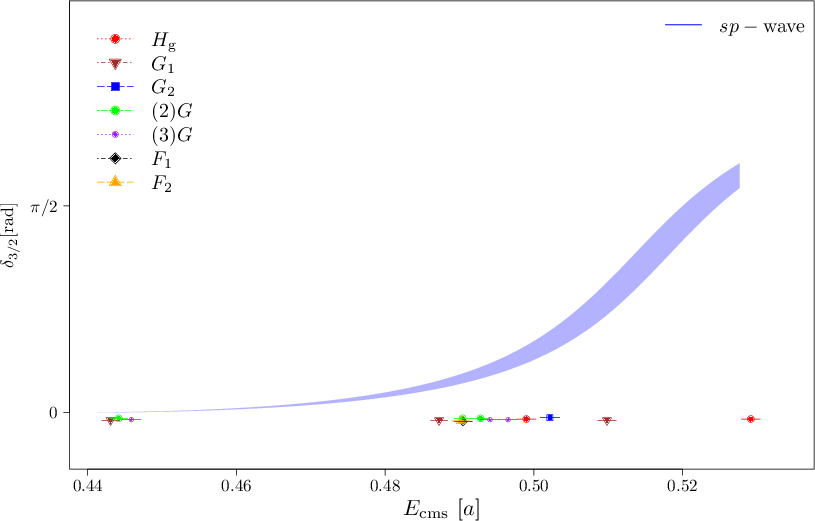
Figure 3: Phase shift for Nucleon-Pion scattering in the Δ channel from Reference [1].