ENVIRONMENT AND ENERGY
MAssive Parallel Approximation of Static and Time-VariablE Reference Surfaces with C1-smooth Finite Element Model Functions
Principal Investigator:
Prof. Dr. Wolf-Dieter Schuh
Affiliation:
University of Bonn, Bonn, Germany
Local Project ID:
MAPSTER
HPC Platform used:
JUWELS CPU of JSC
Date published:
Summary
The Earth is a dynamic system, various physical processes lead to deformations of the Earths surface or mass transport in its interior. Quantifying the changes with the help of measurements is a key task of geodesy, for instance to make signals attributed to climate change visible. For this, reference systems and reference surfaces are required. E.g. sea level rise refers to the so called Mean Sea Surface (MSS), or the geoid as an equipotential surface is required to show mass transport. The reference surfaces can be determined from hundreds of million measurements collected by satellites. Due to the characteristics of the collected data and the complexity of the surfaces, high performance computing is required for the numerical analysis.
Project Description
Introduction and Context
The project is focused on the computation of reference surfaces which are required to quantify temporal changes in the Earth system. Various physical processes lead to mass transport in the Earth system or to a deformation of the Earths’ surface. These changes can be either numerically modeled based on physical laws, e.g. the ocean circulation by oceanographic models, or – as targeted in geodesy – measured. These measurements can then be either used to calibrate or validate the physical models or to identify unknown signals or confirm expected signals.
For deformation studies or mass transport studies, the gravity field of the Earth plays an important role. By definition of physical heights, no water flows between points of same height. Due to an irregular distribution of materials of various density in the Earths’ interior, the gravitational attraction is varying. Therefore, an equipotential surface has a very irregular shape. Its accurate knowledge is required for the definition of height systems and to monitor mass transport relative to the a long term mean. From the static gravity field, the so called geoid can be derived, which shows the deviation of the equipotential surface from a kind of best fit ellipsoid (see Fig. 1). The variations are in the order of ±100 meter. Whereas the dominant features are well known, the fine scale variations are not globally known with the required precision (centimeter level). Therefore dedicated satellite gravity field missions were developed to measure the gravity field from space. With the help of the granted computing time, global gravity field models from satellite missions were computed.
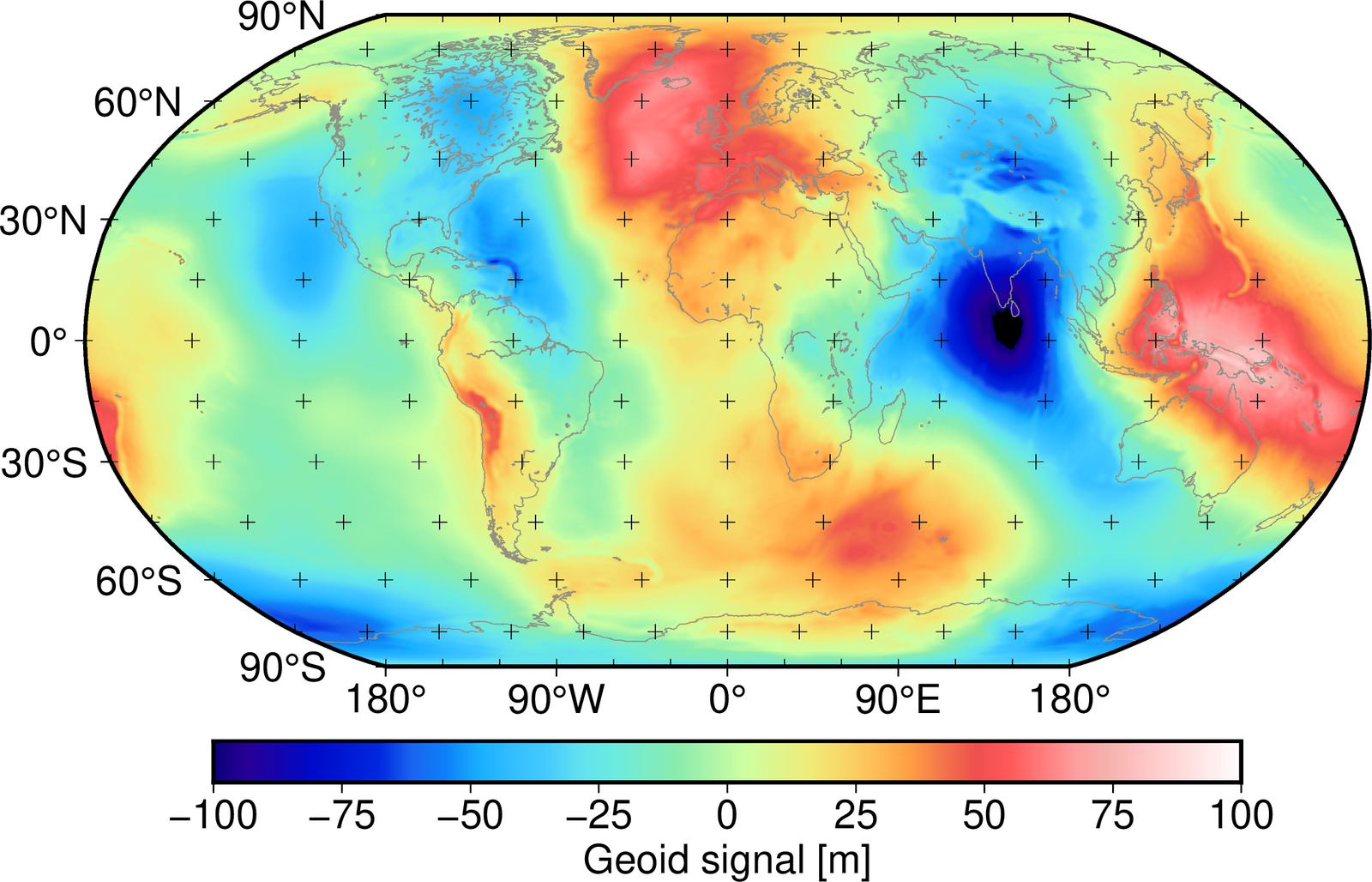
Figure 1: Geoid computed from the spherical harmonics (up to degree and order 200) of the global GOCE-only model GO_CONS_GCF_2_TIM_R6 (https://doi.org/10.5880/ICGEM.2019.003)which was estimated in the project.
To study sea level rise, a long term Mean Sea Surface (MSS) is required to quantify the changes with respect to the mean. The MSS is the second reference surface studied within the project. A global MSS product is depicted in Fig. 2. It is determined from temporally and spatially averaged Sea Surface Height (SSH) measurements taken by radar altimetry satellites since decades. Although its computations seems simple – averaging the measured heights in space and time – the computation is challenging as the data sampling is very irregular in the spatial as well as the time domain. Within the project, a continuous representation of the MSS is proposed, co-estimating the spatio-temporal changes.
Comparing the geoid in Fig. 1 and the MSS in Fig. 2 over the ocean, both reference surfaces seem to correspond. But, when taking the difference and applying some smoothing the third reference surface of interest results, the so called Mean Dynamic ocean Topography (MDT, see Fig. 3). Assuming the Earth in rest and no forces acting on the ocean, it is obvious that the ocean water masses would adjust to the geoid (no water flows). But due to variations in temperature, salinity and forces like winds, the MSS deviates from the geoid. This deviation is defined as the MDT and can be linked to the steady-state ocean circulation. The currents are proportional to the gradient of MDT. Within the project, an approach is developed to jointly estimate both, the geoid and the MDT from SSH and complementary measurements for regional analysis.
Due to a huge number of measurements (hundreds of millions) analyzed, the data characteristics, and a large number of parameters (hundreds of thousands) required to describe the reference surfaces, the applied approaches are computationally challenging and require the use of high performance computing resources.
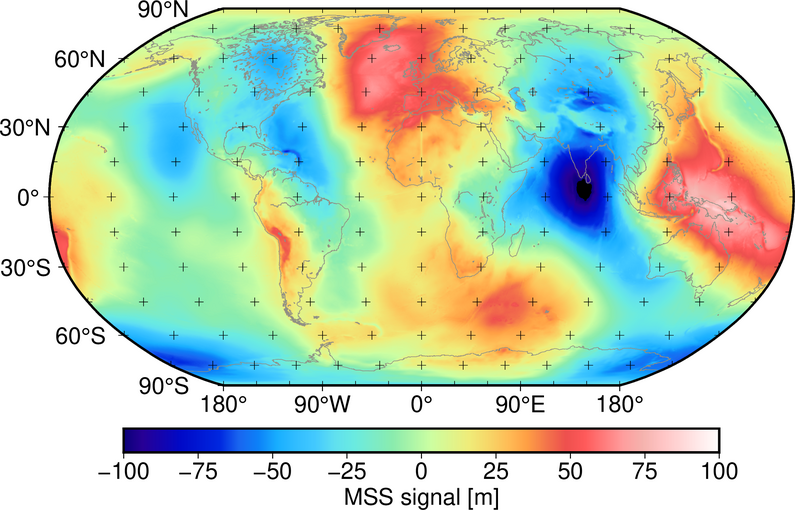
Figure 2: Spatial map of the global mean sea surface from the global model DTU18MSS computed by DTU Space as a global 1’x1’ grid (https://ftp.space.dtu.dk/pub/DTU18/).
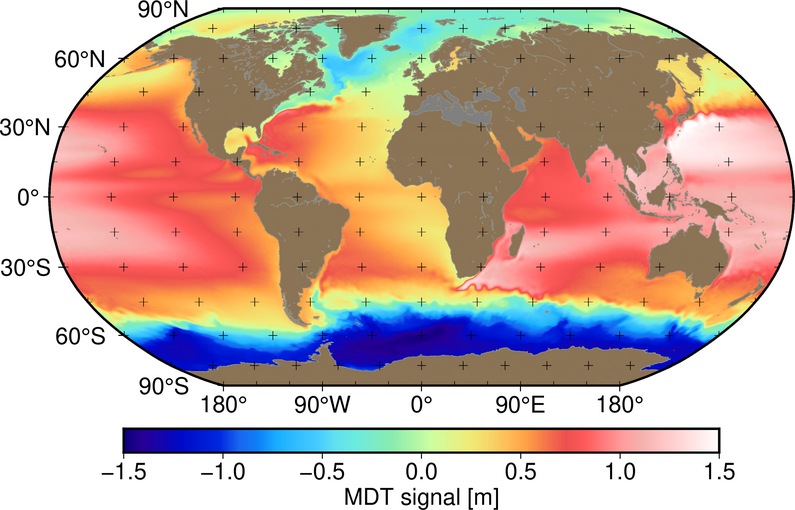
Figure 3: Spatial map of the global mean dynamic ocean topography model MDT-CNES-CLS22 (https://doi.org/10.24400/527896/a01-2023.003) computed by CNES-CLS and provided by AVISO.
Results
Estimated Global Gravity Field Models
One of the dedicated satellite mission for the determination of the Earths gravity field is the Gravity Field and Steady-State Ocean Circulation Explorer (GOCE) realized by the European Space Agency (2009 to 2013) as the first Earth Explorer mission. The main measurement principle of GOCE is gradiometry, i.e. differential gravitational accelerations are measured with a very high precision. Within the project and its predecessor projects, an updated gravity field model from measurements of the GOCE mission were computed. Based on re-calibrated measurements and an improved methodology for modeling the noise characteristics of the measurements, the GO_CONS_GCF_2_TIM_R6 global gravity field model was estimated solely using observations taken by the GOCE satellite [4]. The derived solution is one of the official mission output products.
The gravity field is represented as a spherical harmonic expansion. Additionally, its uncertainty is reflected by a covariance matrix of the spherical harmonic coefficients. It is one of the internationally most accepted GOCE-only models. The performed analysis is computationally demanding as it requires the solution of an ill-posed and highly over-determined system of equations with 440 000 000 equations and 90 000 unknowns. Furthermore, observations from additional satellite missions with different measurement principles are used to determine combined gravity field models, utilizing measurements from multiple satellited yielding higher quality gravity field estimates (GOCO models, [5]).
Approach for Spatio-Temporal Mean Sea Surface Estimation
Although the MSS is ‚just‘ the temporal average of the instantaneous SSH measurements the computation is challenging. This is strongly related to the sampling of the altimetry missions: this are either exact repeat missions, which revisit the same ground location after a few days (10 to 30 days) or geodetic missions with a repeat cycle above a year. Whereas the first have a coarse spatial resolution (80 to 300 km cross track), the later have a cross track spacing of just few kilometers (see Fig. 4). Consequently, for the estimation of an MSS both mission types have to be jointly analyzed over a period of decades. As the number of missions varies over the analysis period, spatial and temporal sampling is inhomogeneous, such that aliasing occurs. Therefore the temporal ocean variability has to be accounted for.
Within the project, a one step procedure is developed, jointly estimating a high resolution MSS parameterized by finite elements and a lower resolution spatio-temporal model for the ocean variability. With the help of the computing time granted in the project, the approach was successfully implemented and tested for regional MSS determination [1, 2].
Figure 4: Zoom to the ground tracks and sea surface height measurements of the exact repeat mission Jason-1 (a) and the geodetic mission Cryosat2 (b) for a one year observation period for a regional study area south of Africa.
Joint Estimation of Regional Geoid and MDT
The geodetic estimation of the MDT tries to separate instantaneous altimetric SSH measurements into the geoid, the MDT, temporal ocean variability and measurement noise. Within the project, an alternative approach was developed to jointly estimate the geoid, the MDT and the temporal ocean variability from SSH observations and complementary data sets [3]. As SSH purely observes the sum of all contributors, the complementary data is essential to solve the separation task.
Due to the formulation of the problem, it is straightforward to include various complementary data sets [6]. In addition to geoid information (e.g. from the global gravity field models discussed above), surface currents measured by drifting buoys, or as studied conceptually in the project Synthetic Aperture Radar derived radial surface velocities determined from a residual Doppler shifts [6] are sensitive to the MDT. The study has shown that the continuous representation of the MDT and the ocean variability with C1-smooth finite elements is well suited and allows to integrate the complementary data.
References
[1] M. Borlinghaus, C. Neyers, and J. M. Brockmann. “Development of a Continuous Spatiotemporal Finite Element-Based Representation of the Mean Sea Surface”. Journal of Geodesy (2023), DOI: 10.1007/s00190-023-01709-1.
[2] M. Borlinghaus, C. Neyers, and J. M. Brockmann. “Refinement of Spatio-Temporal Finite Element Spaces for Mean Sea Surface and Sea Level Anomaly Estimation”. In: X Hotine-Marussi Symposium on Mathematical Geodesy. Ed. by J. T. Freymueller and L. Sánchez. Springer International Publishing, 2023, DOI: 10.1007/1345_2023_205.
[3] J. M. Brockmann, M. Borlinghaus, C. Neyers, and W.-D. Schuh. “On the Coestimation of Long-Term Spatio-Temporal Signals to Reduce the Aliasing Effect in Parametric Geodetic Mean Dynamic Topography Estimation”. In: X Hotine-Marussi Symposium on Mathematical Geodesy. Ed. by J. T. Freymueller and L. Sánchez. Springer International Publishing, 2023, DOI: 10.1007/1345_2023_224.
[4] J. M. Brockmann, T. Schubert, and W.-D. Schuh. “An Improved Model of the Earth’s Static Gravity Field Solely Derived from Reprocessed GOCE Data”. Surveys in Geophysics (2021). DOI: 10.1007/s10712-020-09626-0.
[5] A. Kvas, J. M. Brockmann, S. Krauss, T. Schubert, T. Gruber, U. Meyer, T. Mayer-Gürr, W.-D. Schuh, A. Jäggi, and R. Pail. “GOCO06s – a Satellite-Only Global Gravity Field Model.” Earth System Science Data (2021), DOI: 10.5194/essd-13-99-2021.
[6] C. Neyers and J. M. Brockmann. “Radial Surface Currents from Space: An Opportunity for Mean Dynamic Topography Estimation?” In: Advances in Space Research (2024). DOI: 10.1016/j.asr.2024.05.041.