MATERIALS SCIENCE AND CHEMISTRY
Ab initio Modelling of Iridium Dioxide Nanoparticles as Catalysts for Proton Exchange Membrane Water Electrolysis Cells
Principal Investigator:
Jakob Timmermann
Affiliation:
Chair of Theoretical Chemistry, Technical University of Munich
Local Project ID:
pr53qu
HPC Platform used:
SuperMUC and SuperMUC-NG of LRZ
Date published:
Scientific work and results: Nanoparticle - Compare Wulff structure to optimized geometry
The almost infinite number of possible nanoparticle structures including a variety of energetical similar but structural different minima for each atomic composition seems to prevent a systematic modelling and simulation approach. However in the early 20th century, G. Wulff proposed a simple and systematic way to determine an initial nanoparticle shape (Wulff shape) [1]: for each possible surface (e.g. facet: Miller Index (111), termination: oxygen rich t2) an imaginary plane is shifted along the respective normal vector (in this case n0=[1,1,1]) relative to the surface energy of a periodic slab as shown in I and II of Figure 1. Next the actual nanoparticle is generated based on the Wulff shape, the termination and approximate/required number of atoms. It shall be noted that, as illustrated in IIIa and IIIb of Figure 1, the final Wulff shape might differ from the ideal Wulff shape due to its discretized nature.
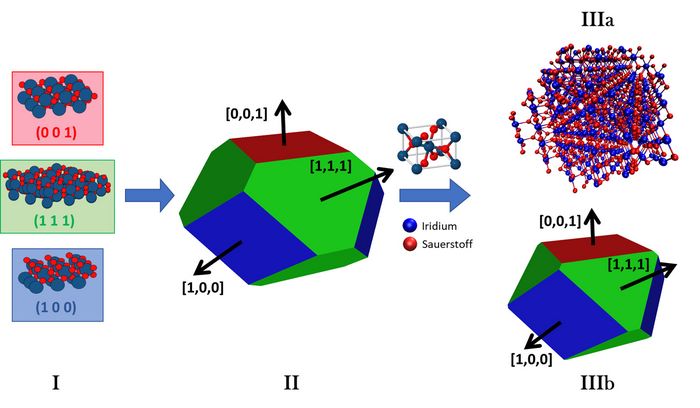
Figure 1: Schematic Wulff construction of iridium dioxide nanoparticles: (I) The energies of (001), (111) and (100) surfaces are calculated. (II) Planes perpendicular to the respective Miller vectors e.g. [1,1,1] are all shifted relative to the surface energies to obtain the Wulff shape. (III) Based on the rutile IrO2 unit cell and according to information about terminations and atom number the Wulff particle (IIIa) is extracted. The applied final Wulff shape (IIIb) is in this case different to the ideal Wulff shape due to the discretized nature of the bulk crystal. © TUM
Prior to this project the surface energies of interest including all low-index Miller facets (e.g. (100), (001), (111) etc.) and terminations necessary to capture any possible Wulff shapes for rutile structured IrO2 have been extracted from periodic slab calculations applying the full-potential density-functional theory code FHI-aims. To capture the working conditions of a PEM cell the energy of each surface has been extracted applying a potential of 1.3 V. In this environment the (111) and (101) facets are predominating irrespective of the chosen termination.
At this point it has to be noted that the actual termination of the surface is a dynamic property which might depend strongly on the acidity and redox properties of the solvent and may even undergo reactions such as adsorption respectively desorption. Such behaviour can only be described by extensive simulations such as DFT molecular dynamics simulations which are, however, way beyond the scope of any short-term project.
Instead the present project is pursuing a different approach:
- Generating mono-surface input structures of different size for all important (111) and (101) facets-termination combinations.
- Performing geometry relaxation calculations for each structure applying the plane wave density-functional theory code CP2K.
- Analysing the relaxed geometries regarding surface reconstruction to verify whether the Wulff construction yields appropriate initial geometries.
Figure 2: The four different surfaces related to the (111) facet from left to right: oxygen deficient (111)-t0, stoichiometric (111)-t1, oxygen rich (111)-t2 and (111)-t-O with an additional oxygen attached to the surface iridium. © TUM
For both facets three different terminations characterized by an increasing number of oxygen atoms can be extracted from the rutile IrO2 bulk crystal, namely: oxygen-deficient (t0), stoichiometric (t1), and oxygen-rich (t2) with the (111)‑terminations illustrated in Figure 2. Moreover, for the (111) facet a termination with an additional oxygen (t‑O) which can’t be extracted directly from the bulk structure but is generated by attaching an additional oxygen to the surface iridium of (111)-t2 has been investigated. This surface is also illustrated in Figure 2. At least two differently sized nanoparticles of each facet-termination combination (surface sequence) have been examined.
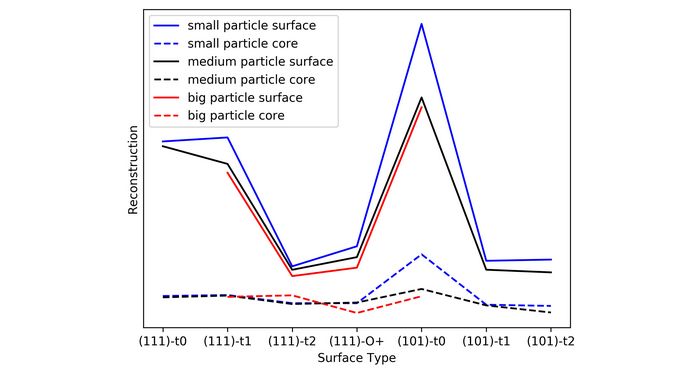
The key results regarding the particle reconstruction are summarized in Table 1 and illustrated in Figure 3. The degree of reconstruction of the different nanoparticles can be compared via the minimal root-mean-square deviation (RMSD) of the initial Wulff structure and the final relaxed geometry. The RMSD value is minimized in a two-step process, at first the two structures are re-centred and then rotated onto each other applying Kabsch [2] and Quaternion [3] algorithm.
Table 1: Number of atoms and minimal root mean square deviation of initial and relaxed geometries (RMSD) of all investigated surface sequences.
Number of Atoms | All atoms | RMSD Surface | Core | |
| (111)-t0 | 301 657 | 4.0 3.6 | 5.0 4.8 | 0.7 |
| (111)-t1 | 201 491 973 | 4.0 3.1 2.7 | 5.1 4:3 4.1 | 0.7 |
| (111)-t2 | 243 565 1087 | 1.3 1.1 1.0 | 1.5 1.4 1.2 | 0.5-0.7 |
| (111)-t-O | 263 607 1159 | 1.6 1.4 1.1 | 2.1 1.8 1.5 | 0.5 0.2 |
| (101)-t0 | 169 521 1173 | 7.5 5.1 4.4 | 8.2 6.2 5.9 | 1.8 0.9 0.7 |
| (101)-t1 | 255 693 | 1.5 1.2 | 1.7 1.4 | 0.45 |
| (101)-t2 | 355 889 | 1.4 1.2 | 1.7 1.3 | 0.4 0.2 |
To provide a more precise evaluation of the degree of reconstruction the procedure is repeated taking only surface atoms respective core atoms into account.
Figure 3 illustrates that the minimal RMSD value though depending on the size of the particle is much more depending on the selected termination. Oxygen rich surfaces (101)-t2, (111)-t2 and (101)‑t‑O as well as the stoichiometric (101)-t1 surface don’t undergo profound reconstruction compared to the corresponding core atoms while the oxygen-poor surfaces especially (101)-t0 are prone to reconstruction.
Figure 3: RMSDconsidering only surface (solid line) or core (dashed line) atoms of all investigated particles. The labels small, medium and big refer to Table1 (e.g. small particles include all structures with less than 450 atoms). © TUM
In conclusion, regarding oxygen saturated respectively oxygen rich particles, the Wulff structures of IrO2 nanoparticles seem to be suitable approximation while oxygen deficient surfaces undergo noticeable reconstruction and nanoparticles including such surfaces have to be handle with special care.
On-going Research / Outlook: Limitations and next steps
Iridium dioxide nanoparticles will be further investigated based on the insights and structures obtained in course of this project.
The very next step is finishing the comparison and performance analysis of AIMS and CP2K calculations which has not been addressed in this report as well as the extraction of edge and vertex energies from the surface sequences in relation to the respective surface frame.
Obviously, the geometry relaxation calculations provide much more information than RMSD values. A detailed analysis of the electronic structure e.g. regarding projected density of state (again considering surface and core atoms separately) is still pending.
Parallel to ongoing analysis of existing data, new simulation protocols shall be developed with special focus on the PEM environment i.e. (implicit) water solvation and/or applied potential to determine to what extent these influence the nanoparticle structure.
Additional References
1. Wulff, G.V., Zur Frage der Geschwindigkeit des Wachstums und der Auflösung der Krystallflächen. Zeitschrift für Krystallographie und Mineralogie. , 1901. 34: p. 449 -530.
2. Kabsch, W., A solution for the best rotation to relate two sets of vectors. Acta Crystallographica Section A, 1976. 32(5): p. 922-923.
3. Walker, M.W., L. Shao, and R.A. Volz, Estimating 3-D location parameters using dual number quaternions. CVGIP: Image Understanding, 1991. 54(3): p. 358-367.
Research Contributors
Anna Anic, Dr. Daniel Opalka (both: Chair of Theoretical Chemistry, Technical University of Munich)
Scientific Contact
Jakob Timmermann
Chair of Theoretical Chemistry
Technical University of Munich
Lichtenbergstr. 4, D-85747 Garching (Germany)
e-mail: jakob.timmermann [@] ch.tum.de
NOTE: This report was first published in the book "High Performance Computing in Science and Engineering – Garching/Munich 2018".
LRZ project ID: pr53qu
July 2020