MATERIALS SCIENCE AND CHEMISTRY
Emergent Locality in Quantum Systems with Long Range Interactions
Principal Investigator:
Fabien Alet (1) and David J. Luitz (2)
Affiliation:
(1) Centre national de la recherche scientifique (CNRS), Toulouse University, France, (2) Max Planck Institute for the Physics of Complex Systems (MPIPKS), Dresden, Germany
Local Project ID:
PP16153659
HPC Platform used:
Hazel Hen of HLRS
Date published:
How fast can information travel in a quantum system? While special relativity yields the speed of light as a strict upper limit, many quantum systems at low energies are in fact described by nonrelativistic quantum theory, which does not contain any fundamental speed limit. Interestingly enough, there is an emergent speed limit in quantum systems with short ranged interactions which is far slower than the speed of light. Fundamental interactions between particles are, however, often of long range, such as dipolar interactions or Coulomb interactions. A very-large scale computational study performed on Hazel Hen revealed that there is no instantaneous information propagation even in the presence of extremely long ranged interactions and that most signals are contained in a spatio-temporal light cone for dipolar interactions.
Full Report
The best quantum theory for high energy particles, such as they appear in cosmic radiation or in particle accelerators like CERN’s large hadron collider, is based on Einstein’s theory of special relativity and includes the speed of light as a strict speed limit for the transmission of information. However, most quantum systems of many particles which can be produced in laboratories are at much lower energies and therefore can exhibit different physics. It turned out that there is an additional quantum speed limit for quantum systems with short ranged interactions between many particles, for example the interaction between electrons in solids, which is screened by the presence of many other electrons. For such systems, Lieb and Robinson proved in a seminal work in 1972 that there is an emergent speed limit slower than the speed of light, which limits the maximal information transport in quantum many-body systems. This plays a crucial role for the buildup of correlations of particles, for how fast a quantum system can reach thermal equilibrium, as well as for practical implementations of quantum computers as this bound limits the loss of quantum information.
Today there is an increasing interest in quantum systems which exhibit long range interactions between their constituents, since they can be manufactured in experiments with ultracold quantum gases of atoms with dipolar interactions. One recent example are experiments with exotic Dysprosium atoms, which have a large magnetic moment and exhibit long ranged dipolar interactions. For such systems, we currently have limited knowledge for how fast quantum information can travel. The current computational study addressed this issue by an exact numerical simulation of two generic models of strongly interacting quantum systems with long ranged interactions.
Models of quantum matter with many-body interactions represent a formidable challenge since they are not analytically solvable and experiments are currently not precise and universal enough to provide a universal answer. Therefore it is of crucial importance to solve these models numerically with state of the art computational techniques. This is the aim of the STIDS project. The main numerical challenge is that the complexity of the calculation grows exponentially with the number of particles in the system: in a nutshell, the complexity is (at best) doubled when adding one more particle.
In the precise study of information propagation, the long-range nature of the interactions leads to very fast dynamics and requires to simulate systems as large as possible. The work of the STIDS team has pushed calculations on HLRS’s Hazel Hen supercomputer located in Stuttgart to the limit of what is currently feasible, reaching 15 quantum particles on 31 lattice sites. These simulations are converged in terms of system size, meaning that the results do not change if the system size is further increased.
The complete description of the problem is encoded in the wave function of the quantum many-body system, which time evolution is obtained through the solution of the Schrödinger equation. Storing and computing this wave-function requires a massive amount of computer time and memory (RAM) for these large systems. The largest calculations for this project required more than 10TB of memory and 100 nodes of the Hazel Hen supercomputer in parallel for a single calculation. These resources were crucial for reaching the largest system sizes to prove that the findings are converged with the number of particles.
The main findings for the one dimensional systems of this study are: 1. There is an emergent speed limit for systems with long range interactions which decay with distance r faster than 1/r. This leads to a “light cone”, a region of causality in space-time outside of which no quantum communication can occur. 2. For interactions which decay slower than 1/r with distance, there is a causal region with power law envelope, which excludes immediate quantum communication even for very long-range interactions. 3. All quantum speed limits known so far for long ranging interactions are not tight, i.e. there are actual limits which are even slower than previous work suggested.
In conclusion, the present numerically exact study represents considerable progress on the question of how fast quantum information can travel in solids or ultracold atomic gases. These results are of fundamental importance for a deeper understanding of thermalization and of the time scales for the generation of quantum entanglement, the resource of quantum computation.
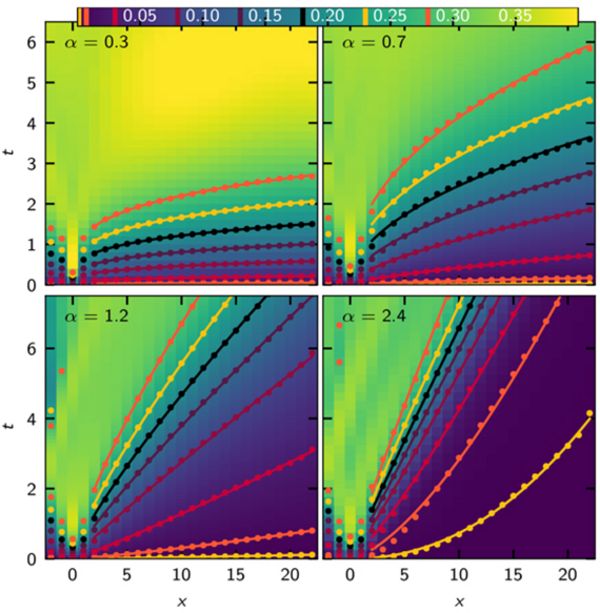
The colorscale quantifies how much information has travelled in a quantum system with long ranging interactions between particles decaying with distance as 1/rα over a distance x in time t. Larger α correspond to faster decay and therefore shorter-range interactions. The solid lines represent contour lines and correspond to a fixed information content. For α>1 a linear light cone structure emerges for most of the information content with some leaking of very small amounts of information which spreads faster.
Copyright: CNRSReference for the present research:
Emergent locality in systems with power-law interactions. David J. Luitz and Yevgeny Bar Lev. Phys. Rev. A 99, 010105(R) – Published 30 January 2019 -- DOI: https://doi.org/10.1103/PhysRevA.99.010105
Contact for the present research:
David J. Luitz
Max Planck Institute for the Physics of Complex Systems
Nöthnitzer Straße 38, D-01187 Dresden (Germany)
e-mail: dluitz [at] pks.mpg.de
NOTE: This project was made possible by PRACE (Partnership for Advanced Computing in Europe) allocating a computing time grant on GCS HPC system Hazel Hen of the High Performance Computing Center Stuttgart (HLRS), Germany.
HLRS project ID: PP16153659
February 2019