MATERIALS SCIENCE AND CHEMISTRY
Molecular and Multiscale Simulation of Crystal Growth from Solution
Principal Investigator:
Heiko Briesen, Ekaterina Elts, Anthony Reilly
Affiliation:
Chair of Process Systems Engineering, Technical University of Munich (Germany)
Local Project ID:
pr58la
HPC Platform used:
SuperMUC and SuperMUC-NG of LRZ
Date published:
Introduction
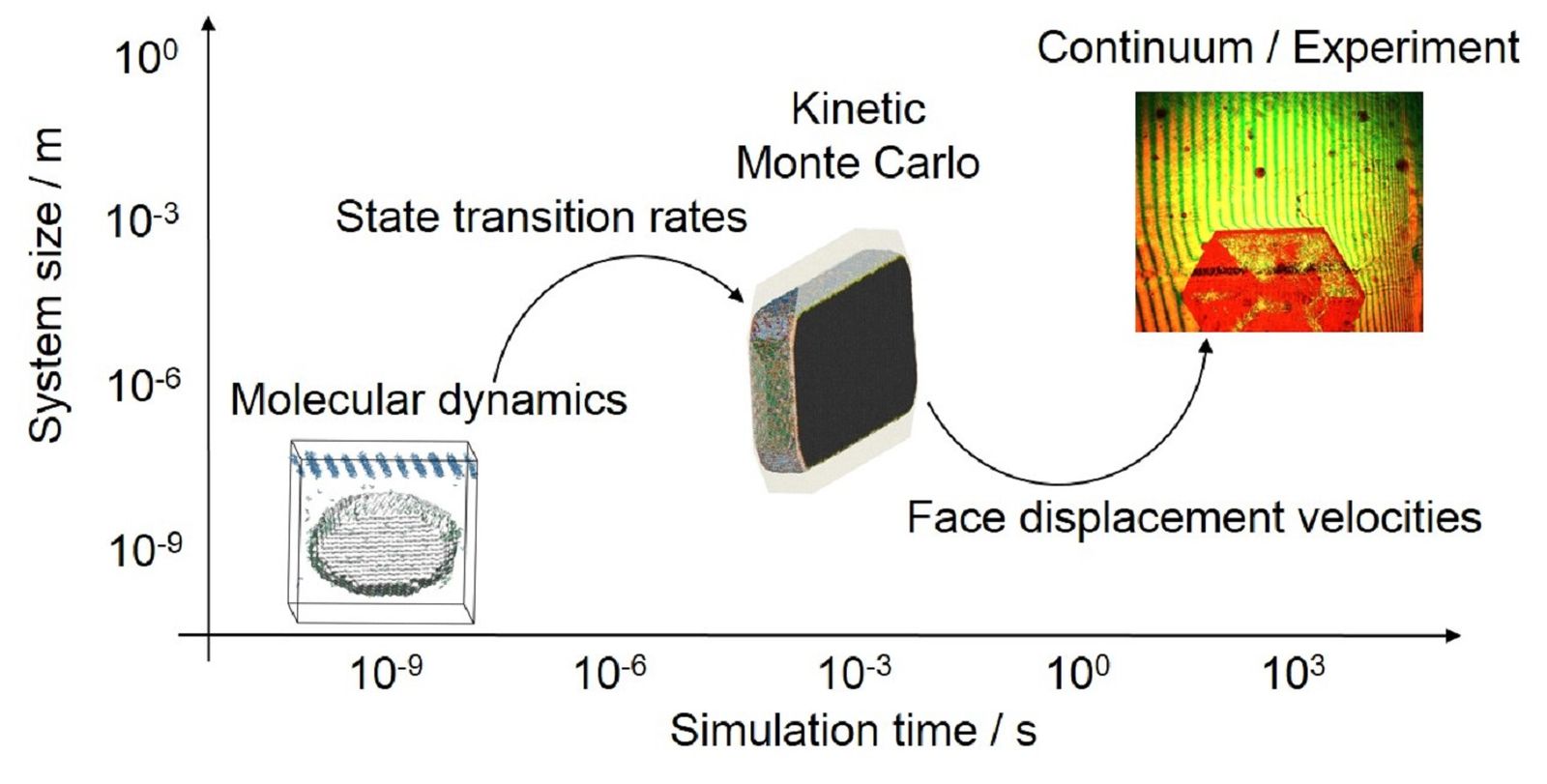
Fundamentally, the process of crystal growth and dissolution occurs on the molecular level, which concerns crystal packing, integration and disintegration as well as diffusion of molecules. However, not only nanoscale but also microscopic (as concerns crystal surface structures and growth/dissolution mechanisms) and macroscopic (as concerns face displacement, concentration effects, and crystal morphology) aspects are important factors in crystal growth and dissolution processes. Thus, to study crystal growth or dissolution one needs a multiscale simulation approach that integrates all these aspects in one unified simulation framework (see Fig. 1). The standard simulation technique for modeling molecular-level behavior to reveal how the molecular details influence the growth and dissolution kinetics is molecular dynamics (MD). However, MD can, at most, only probe behavior on the nanometer and nanosecond scale. In our multiscale approach, this technique is used to calculate the rate constants for all possible growth and dissolution events. Thus, it is essential that a wide range of systems is simulated and analyzed. The obtained rate constants are then fed to the kinetic Monte Carlo (kMC) method capable of studying growth and dissolution on the microscale.
Methods
To obtain the information required for the kMC method MD simulations of crystals in experimentally determined shapes are performed. Such systems usually comprise many thousands of atoms and to simulate the growth or dissolution of such systems many 10’s or even 100’s of nanoseconds worth of data must be collected. This makes the work computationally very demanding. In Fig. 2, for example, aspirin nanocrystal simulated by our group is shown. The size of the nanocrystal was around 10×15×8 nm3 and consisted of a total number of 4079 ASA molecules, the simulation box contained 84160 molecules of water. The simulation of 280 ns took about 250 000 CPU hours.

Figure 2: Structure of aspirin crystals as proposed in the literature (a), as seen in our experiment (b), and as implemented in the MD simulation (c). Red points above the nanocrystal in panel c represent sticky dummy atoms introduced to ensure constant undersaturation and, thus, continuous dissolution during MD simulations [4].
To analyze nanocrystal MD simulations and calculate rates for individual transition events, like incorporation or dissolution of a solute molecule into/from a particular crystal face or edge, crystal molecules are classified into different edge and surface categories, as demonstrated in Fig. 3.
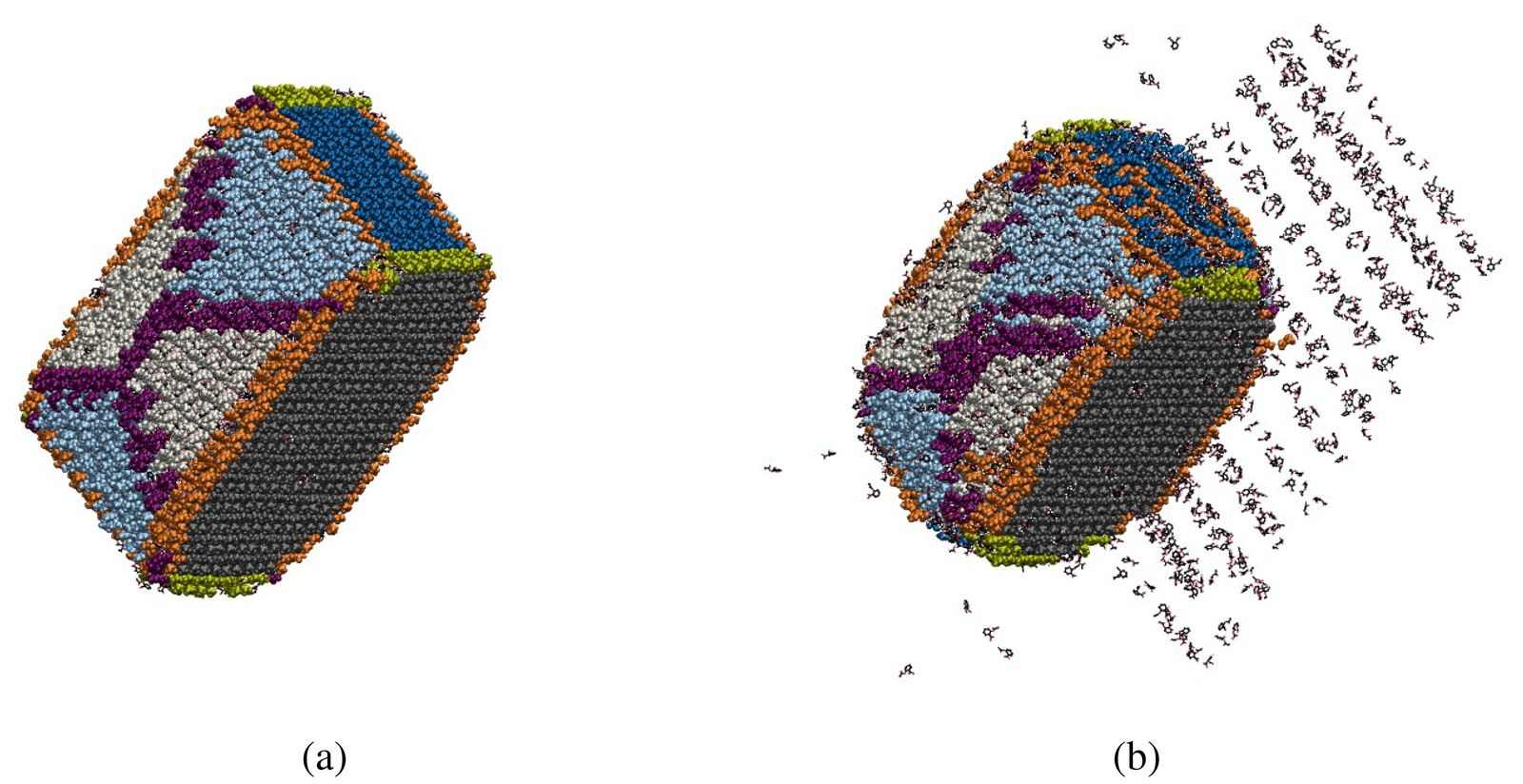
Figure 3: Result of state classification applied to an aspirin nanocrystal (a) at the beginning of the MD simulation and (b) after 280 ns of simulation. The molecules located at flat faces are gray for the (100) face, blue for the (001) face, light blue for the (011) face, and light gray for the (110) face. Molecules located on edges formed by the intersection of single-indexed faces are indicated in light green, and purple is used to show molecules on the edges formed by the intersection of double-indexed faces. Orange indicates molecules on the edges formed by single- and double-indexed faces. Water and sticky dummy atoms are not shown [6].
Based on the growth and dissolution rates determined from MD simulation, kMC simulations can be performed. In a kMC approach, dissolution and growth of the crystal are considered as a competition of different processes, such as integration from solution, dissolution into solution and surface diffusion of the molecules. Since only these slow events that are able to change the macroscopic state of the system are taken into account in kMC, calculations are much faster than for explicit MD simulations. Thus, kMC can model much larger systems and for much longer time scales. However, kMC simulation could lead to the formation of new crystal faces and edges, which have not been seen in MD simulations. To obtain the rates for the processes on these new faces and edges additional MD simulations with the correspondingly changed crystal structure are often needed. Moreover, in case it is not possible to obtain statistically meaningful transition rates for surfaces, it is helpful to introduce some minor defects onto these surfaces and to perform a systematic study of their influence on the growth and dissolution rates. Thus, to obtain all rates for kMC simulations several starting configurations need to be simulated. According to the basic assumption of the elaborated multiscale approach, individual molecular steps are independent from each other and one can combine the results of multiple independent MD simulations to calculate transition rates. All these MD simulations are extremely computationally complex and executing them on desktop class computers would not be possible. Thus, it was absolutely crucial to employ supercomputer facilities to be able to achieve the research goals in a reasonable time. MD code Gromacs (www.gromacs.org) with its well-tested scaling on the LRZ system was perfectly suited for our simulations. It features efficient algorithms for dealing with long-range interactions (e.g. particle-mesh Ewald method), as well as MPI and thread parallelization using domain and particle decomposition.
Results
The results of our investigations obtained using LRZ resources during the time frame from 27.06.2011 until 31.12.2020 are published in peer-reviewed articles presented below [1-10]. With the support of computing resources on SuperMUC and SuperMUC-NG of LRZ our team has managed to develop a multiscale approach for studying crystal growth and dissolution and to demonstrate how one can bridge a gap from molecular resolution to experimental time and size scales [1-2, 6-8]. Different active pharmaceutical ingredients like Aspirin [3-4, 6-8], Paracetamol [3, 5, 9], Ibuprofen [3] and Glycine [10] were simulated. Based on the simulation data obtained on SuperMUC and SuperMUC-NG we were able to gain a better overall understanding of the crystal growth and dissolution processes [3-4,10] and to develop some processing and analysis algorithms [5, 9] needed to extract process rates for parametrization of the kMC method. We demonstrated the success of our multiscale approach on the example of aspirin crystal dissolution in water, where our simulation results were in very good agreement with experimental results [7-8].
This video shows the dissolution of aspirin crystal in water during 280 ns of molecular dynamics simulation. Molecules belonging to different faces and edges are shown in different colors. Dissolved aspirin molecules accumulate on the right side due to the sticky dummy atoms introduced to the system to ensure constant undersaturation and, thus, continuous dissolution during the simulation. Water and sticky dummy atoms are not shown for clarity. It can be seen that the resulting crystal is of comparable size with the initial crystal. The crystal bulk remains basically unchanged for the time simulated. However, numerous molecules left the nanocrystal during the simulation making it possible to calculate the disintegration rates needed for kMC simulations. © TUM
Publications as an outcome of the HPC project
- Reilly, A. and Briesen, H. Modeling crystal growth from solution with molecular dynamics simulations: Approaches to transition rate constants. J. Chem. Phys. 2012; 136: 034704.
- Reilly, A. and Briesen, H. A detailed kinetic Monte Carlo study of growth from solution using MD-derived rate constants. J. Cryst. Growth 2012; 354: 34-43.
- Greiner, M., Elts, E., Schneider, J., Reuter, K. and Briesen, H. Dissolution study of active pharmaceutical ingredients using molecular dynamics simulations with classical force fields. J. Cryst. Growth, 2014; 405: 122-130.
- Greiner, M., Elts, E. and Briesen H. Insights into Pharmaceutical Nanocrystal Dissolution: A Molecular Dynamics Simulation Study on Aspirin. Mol. Pharmaceutics, 2014; 11: 3009-3016.
- Elts, E., Greiner, M. and Briesen, H. Data Filtering for Effective Analysis of Crystal–Solution Interface Molecular Dynamics Simulations. J. Chem. Theory and Comput. 2014; 10:1686-1697.
- Elts, E., Greiner, M. and Briesen, H. Predicting Dissolution Kinetics for Active Pharmaceutical Ingredients on the Basis of Their Molecular Structures. Cryst. Growth Des. 2016; 16: 4154–4164.
- Greiner, M., Choscz, C., Eder, C., Elts, E. and Briesen H. Multiscale modeling of aspirin dissolution: From molecular resolution to experimental scales of time and size. CrystEngComm 2016; 18: 5302–5312.
- Elts, E., Greiner, M. and Briesen, H. In-silico Prediction of Growth and Dissolution Rates for Organic Molecular Crystals: A Multiscale Approach. Crystals 2017; 7: 288.
- Elts, E. and Briesen, H. Capturing Crystal Shape Evolution from Molecular Simulations. J. Chem. Inf. Model., 2020, 60(12): 6109-6119
- Elts, E., Luxenburger, F. and Briesen, H. Influence of Monovalent Salts on Glycine Crystal Growth from Aqueous Solution: Molecular Dynamics Simulations at Constant Supersaturation Conditions, 2021, accepted for the Journal of Physical Chemistry B.
Research Team:
Heiko Briesen(PI), Ekaterina Elts(PI), Maximilian Greiner, Frederik Luxenburger, Anthony Reilly
all: Technical University of Munich, Chair of Process Systems Engineering (Germany)
Scientific Contact:
Prof. Dr.-Ing. Heiko Briesen
Chair of Process Systems Engineering
Technical University of Munich
85354 Freising
Germany
email: heiko.briesen [@] mytum.de
local project ID: pr58la
December 2021