MATERIALS SCIENCE AND CHEMISTRY
Controlling Nano-Scale Friction Through Phase Transitions
Principal Investigator:
Carlo A. Pignedoli
Affiliation:
Empa Swiss Laboratories for Materials Science and Technology Dübendorft (Switzerland)
Local Project ID:
pr89mi
HPC Platform used:
SuperMUC of LRZ
Date published:
The ability to control and manipulate frictional forces at the nanoscale is extremely important for technology, being closely tied to progress in transportation, manufacturing, energy conversion, and lubricant consumption, impacting on innumerable aspects of our health and environment. In recent years a lot of effort has been devoted to gain control of friction at both the macroscopic and microscopic scale. However, most of the employed techniques cannot be straightforwardly extended to the nanoscale, where a flexible and almost cost-free way to dynamically tune friction forces is still lacking.
The flexibility of selected physical properties of the sliding bodies, necessary to actuate a dynamical control of friction, might be provided by the occurrence of a phase transition. A few evidences of this possibility can already be found in literature, and are related to the development of atomic force microscopy (AFM), a quickly improving experimental tool that allows to study, using nanosized oscillating tips, surface properties by sampling contact and non-contact forces down to the atomic scale.
The transition to a superconducting state strongly alters the properties of the electronic degrees of freedom and thus the way the energy is dissipated through them. As a result the non-contact dissipation of a tip oscillating close to a NbSe2 surface has been found to undergo a strong drop crossing the critical temperature Tc for the onset of superconductivity [1]. Oppositely polarized domains in a ferroelectric medium give rise to very different energy dissipation when perturbed with an AFM tips both in contact and non-contact mode, and this effect has been used for long time to image domains and to study the their dynamics at surfaces [2] but never exploited in the converse way, i.e. to tune dissipation and friction.
Recently a team of scientists of the Empa Swiss Laboratories for Material Science and Technology demonstrated the possibility to control nanofriction by switching the order parameter of a structural phase transition [3]. Friction force microscopy (FFM) experiments on a model ferro-distortive substrate have been simulated, showing a non-monotonic behavior of friction as a function of the substrate temperature, broadly peaking at Tc. Besides this unusual feature (stick-slip friction of a single contact on ordinary substrates is known to decrease monotonically unless multiple slips occur), below Tc, the frictional response is found to depend strongly on the substrate distortive order parameter: different values of the substrate distortion can give rise to a very different friction force. Acting now with an external stress field the distortive order parameter of the substrate can be changed reversibly and dynamically, increasing or decreasing the frictional properties of the substrate.
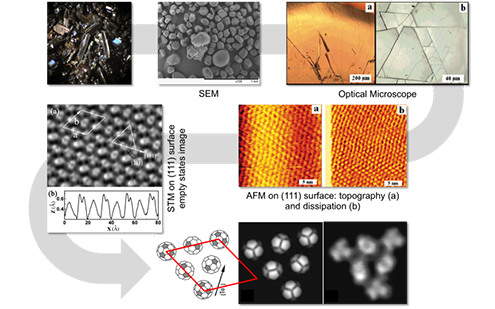
Figure 1: (111) Fullerite (top left) seen through a scanning electron microscope (top center) and a optical microscope (top right). Fullerite (111) surface as revealed by scanning tunneling microscopy (bottom left) and atomic force microscopy.
Copyright: Empa Swiss Laboratories for Material Science and Technology

Sketch of the simulated sliding experiment.
Copyright: Empa Swiss Laboratories for Material Science and Technology
The goal of this project, which was made possible through the Partnership for Advanced Computing in Europe, PRACE, was to identify a real material hosting a structural phase transition in a range of parameters accessible to the standard experimental techniques. To this aim, a practical structural phase transition to look at is the rotational melting occurring near 260 K in pristine C60 molecular crystals (aka Fullerite, see Figure 1 for a portrait of its 111 surface). Such first order phase transition leads from an ordered structure with locked fullerene at low temperatures, to an angular disordered phase with almost freely rotating fullerenes at high temperatures. Recent measurements have indicated a sharp drop of tip adhesion and of AFM sliding friction in connection with this bulk transition [4], However the explanation given for this strong frictional drop is in open contradiction with thermodynamics, as it is immediately visible from a comparison with the cohesive energy of the Fullerite crystal available in the literature. Despite the great importance that the measured frictional drop can have in the control of friction, no theoretical explanation or simulation data are available for the tribological properties of this system.
Using classical molecular dynamics the scientists simulated the pull-off and sliding friction experiments in presence of the rotational melting phase transition. The researchers started reproducing the bulk and surface rotational melting transition, to this aim the potential by Sprik et al. [5] proved to be best solution. This potential is constituted by a Lennard-Jones short range term plus a long range coulombic interaction. Every C60 molecule is treated as a rigid body with 90 interaction centers placed on every carbon atom and on every double bond, to mimic the charge delocalization. Finite size effects are known to inhibit the occurrence of the phase transitions thus, to have a satisfactory description of rotational melting, working with large systems is inevitable, as a typical simulation box contains 16x16x17 fullerenes, i.e. ~400000 interacting particles. As the scientists simulate pull-off and sliding friction experiments they act with an external driving force on the systems. The work done by this force increases the internal energy and, in order to reach a steady state and to prevent the system from blowing up, the excess energy must be disposed off with a thermostat.
In this configuration pull-off and friction forces can increase by an order of magnitude. In conclusion, the phase transition, i.e. the rotation of the C60 molecules, is not directly responsible for the drastic change in the frictional properties of the Fullerite surface, it rather triggers a change in the contact geometry between the tip and the surface. The possibility to control the contact geometry, the commensurability and thus the frictional properties of a surface through the occurrence of phase transitions deserves further investigation being of great potential impact in the field of nanomanipulation and motion control.
The molecular dynamics simulations have been performed with the LAMMPS code [7] an open source state of the art code specifically designed for HPC purposes. The typical production run required 4096 cores for 24-48 hours. HPC system SuperMUC of GCS member centre Leibniz Supercomputing Centre (Garching near Munich) served as computing platform for this project.
New experiments to probe the dissipation of Fullerite across its rotational melting transition with non-contact AFM are ongoing at Empa, in the group of professor H.J. Hug. From the theoretical side new simulations will be carried out to understand how to promote or inhibit the occurrence of the phase transition thus gaining a dynamical control of the friction coefficient, this could be in principle achieved applying an external pressure. Interesting is also the perspective of tailoring the critical temperature by filling the fullerenes with molecules or increasing the number of carbon atoms per molecule.
References and Links
[1] M. kisiel, E. Gnecco, U. Gysin, L. Marot, S.Rast, E. Meyer, Nat. Mater. 10, 119 (2011)
[2] A.K. Taganstev , L.E. Cross and J.Fousek “Domains in Ferroic Crystals and Thin Films” Springer (NY) (2010)]
[3] A. Benassi, A. Vanossi, G.E. Santoro, E. Tosatti Phys Rev Lett. 106, 256102 (2011)
[4] Q. Liang, H. Li, Y. Xu, X. Xiao J. Phys. Chem. B 110, 403 (2006)
[5] M. Sprik, A. Cheng, M.L. Klein J. Phys. Chem. 96, 2027 (1992)
[6] A. Benassi, A. Vanossi, G.E. Santoro, E. Tosatti Phys. Rev. B 82, 81401 (2010)
[7] lammps.sandia.gov
More info about this research on nanoscale friction and dissipation at: https://sites.google.com/site/benassia/
Scientific Contact:
A. Benassi and C.A. Pignedoli
Computational Material Science
Empa Swiss Laboratories for Material Science and Technology
Überlandstrasse 129, CH-8600 Dübendorf/Switzerland
e-mail: Carlo.Pignedoli@empa.ch