MATERIALS SCIENCE AND CHEMISTRY
EXASTEEL - Bridging Scales for Multiphase Steels
Principal Investigator:
Prof. Oliver Rheinbach
Affiliation:
Technische Universität Bergakademie Freiberg, Germany
Local Project ID:
chfg01
HPC Platform used:
JUWELS CPU, JUQUEEN and JURECA VIS at JSC
Date published:
Abstract/Teaser
The project "High performance computational homogenization software for multi-scale problems in solid mechanics" focusses on simulating Advanced High-Strength Steels (AHSS) using computational methods that consider the microscale grain structure. The virtual laboratory relies on high-performance computing and robust numerical methods to predict steel behavior before experimental testing. Computational homogenization reduces the number of degrees of freedom drastically and introduces natural algorithmic parallelism. The scalability of new nonlinear solution methods, as well as the FE^2 software FE2TI was demonstrated under production conditions. A complete virtual Nakajima test was performed leveraging the power of modern supercomputers.
1 Introduction
The development of tailor-made materials through computational simulation is crucial for progress and sustainability. Thanks to the combination of the unprecedented computing power of modern supercomputers such as the one at Julich Supercomputing Centre and the advancement of new computational simulation algorithms and software, we can anticipate a near future where tailor-made materials make our everyday lives more sustainable, efficient, and progressive.
An example of such materials are Advanced High-Strength Steels (AHSS), which offer a powerful blend of strength and flexibility, making them vital, e.g., in the automotive industry, particularly for crash-sensitive vehicle parts. Dual-phase (DP) steel, a type of AHSS, stands out thanks to its exceptional microscale grain structure. In essence, DP steel combines a softer, polycrystalline ferritic base with harder martensitic inclusions, creating a non-uniform material. This microstructure plays a crucial role in steel quality, making it essential to consider when computing stress and strain in deformation simulations. Similar techniques apply for other high-performance composite materials.
The Nakajima test is a common experimental method used to assess the strength of specific steel types, such as newly developed dual-phase (DP) steel. In this test, a steel sample is secured between a blank holder and a die, while a hemispherical punch is pressed into the sheet from below until it cracks. This process is repeated with varying sample geometries, and the deformation and stress within the sheet are analyzed just before the crack appears. A forming limit diagram (FLD) then consolidates the steel's maximum formability based on the different stress states observed in the experiments (see Fig.1 for a schematic representation of the Nakajima test).
The HFG01 project aims to simulate the Nakajima test in a virtual laboratory, taking into account the crucial microstructure of dual-phase steels. This is achieved through high-performance computing and highly scalable, robust numerical algorithms. By using a virtual steel laboratory, it becomes possible to predict the behavior of specific steel designs before they are produced for costly experimental testing.

Fig. 1: Schematic view of the Nakajima test. Different metal sheets (left) are deformed by a spherical punch until a crack occurs (middle). Finally, the resulting maximal stresses and strains of the different sheets are used to build a FLD (right), which describes the formability and robustness of the specific steel.
2 Methods, Algorithms, and Implementation
For the simulation of the Nakajima test, the different sample sheets are discretized with finite elements and a simple contact algorithm is used to drive the spherical punch virtually into the steel. To incorporate the microscopic structure of the specific DP steel, the computational homogenization approach FE^2 is used.
2.1 Homogenization with the FE^2 Approach
The microscopic structure of the DP steel cannot be implemented directly by resolving it on the scale of the metal sheet. On the one hand, the exact microstructure of the complete metal sheet is unknown and on the other hand this approach would lead to systems of equations, which are too large to be solved efficiently, even for state-of-the-art supercomputers. Instead, the computational homogenization approach FE^2 is used, which helps to reduce the degrees of freedom of the complete problem and introduces a natural algorithmic parallelism. It has to be assumed, that a small cubical section of the steel can be found, which is representative for the typical microstructure of the specific steel. This representative volume element (RVE) is used to compute an average stress answer to a given deformation in several locations of the macroscopic problem or, more precisely, in any Gaussian integration points of the macroscopic finite elements. In other words, in the FE^2 method, the steel sheet on the macroscopic level is resolved without considering the microstructure, but in each integration point an RVE is attached; see also Fig. 2 for a schematic view of the FE^2 approach. Simulating the RVEs gives the stress reply to any macroscopic deformation state and drives the deformation evaluation of the whole process. All the RVEs are solved in parallel and independently, which results in a highly parallel scalable algorithm. Communication only occurs during the macroscopic solution in each step of the algorithm. Nonetheless, the FE^2 approach is very expensive, since many RVEs have to be solved many times. This makes the use of modern supercomputers and their parallelism indispensable.
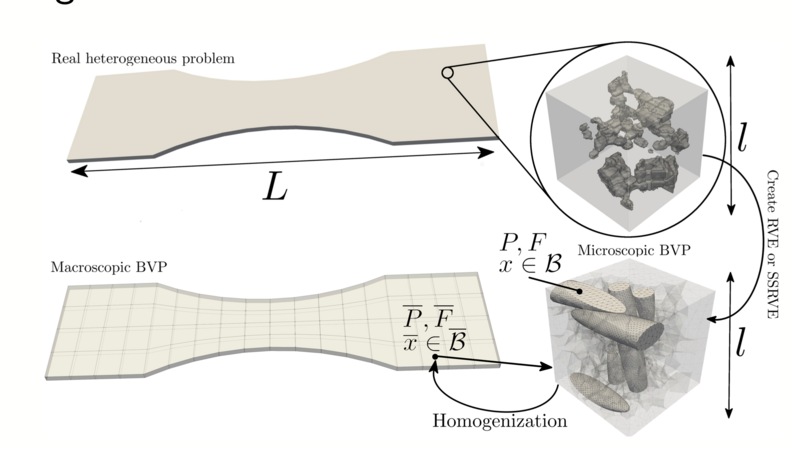
Fig. 2: Schematic view of the FE^2 approach
2.2 State-of-the-Art Domain Decomposition Solvers
For large RVEs or macroscopic geometries, parallel domain decomposition methods (DDMs) are employed to enhance parallelization and speed up computations. In DDMs, the computational domain, which includes the RVE and/or metal sheet geometry, is divided into several non-overlapping subdomains. Each subdomain is assigned to a parallel resource, allowing for rapid, simultaneous calculations. Depending on the specific domain decomposition algorithm, an iterative process is utilized to ensure that local subdomain solutions converge to the global solution of the original problem. In this project, robust nonlinear versions of the FETI-DP (Finite Element Tearing and Interconnecting – Dual Primal) and BDDC (Balancing Domain Decomposition by Constraints) domain decomposition methods have been developed and implemented [3,4].
2.3 Parallel Implementation
The FE^2 method and nonlinear FETI-DP and BDDC are implemented using the open source software library PETSc (Portable, Extensible Toolkit for Scientific Computation) using C/C++. The resulting software package FE2TI has shown to be scalable up to 1 million parallel MPI ranks. Recently, also a hybrid MPI/OpenMP parallelization was included. Parallel file I/O is implemented using HDF5. The FE2TI package contains a contact implementation on the macroscopic scale and an interface to the material library of FEAP.
3 Results
During the EXASTEEL project, part of DFG’s priority program 1648 Software for Exascale Computing (SPPEXA), and the accompanying computing time project hfg01 on JUQUEEN and JUWELS, many goals have been reached. For example, the scalability of newly developed nonlinear FETI-DP and BDDC methods was proved on JUQUEEN and JUWELS (see [3,4]) as well as the scalability of FE2TI under production conditions (see [2]), that is, using realistic steel microstructures and a realistic modelling of the behavior of the ferritic and martensitic phases on the microstructure, using complicated macroscopic geometries and large deformations on the macroscopic scale, and writing all results on micro- and macroscale to the file system. In Fig. 3, a weak scaling study of FE2TI on JUQUEEN is shown, using algebraic multigrid (AMG) as a macroscopic solver. Finally, a complete Nakajima test was performed in our virtual laboratory using the FE2TI software; see Fig. 4. All simulations to obtain the virtual FLD have been performed on the JUWELS supercomputer. More details o the virtual laboratory using FE2TI can be found in [1,2,5].
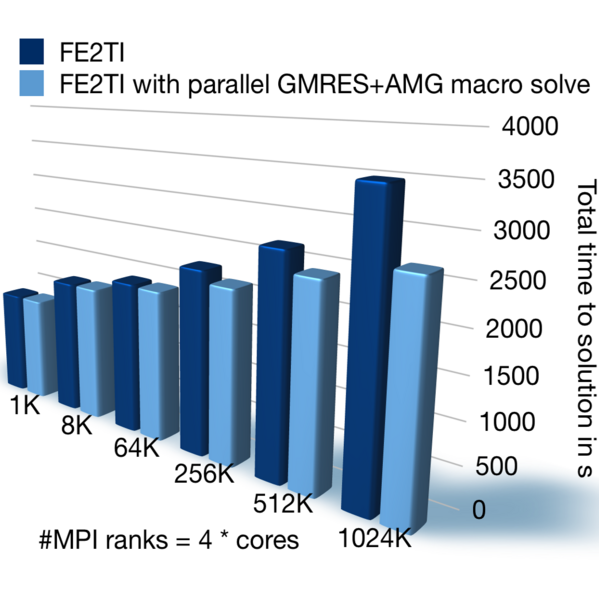
Fig. 3: Weak scaling of FE2TI on JUQUEEN
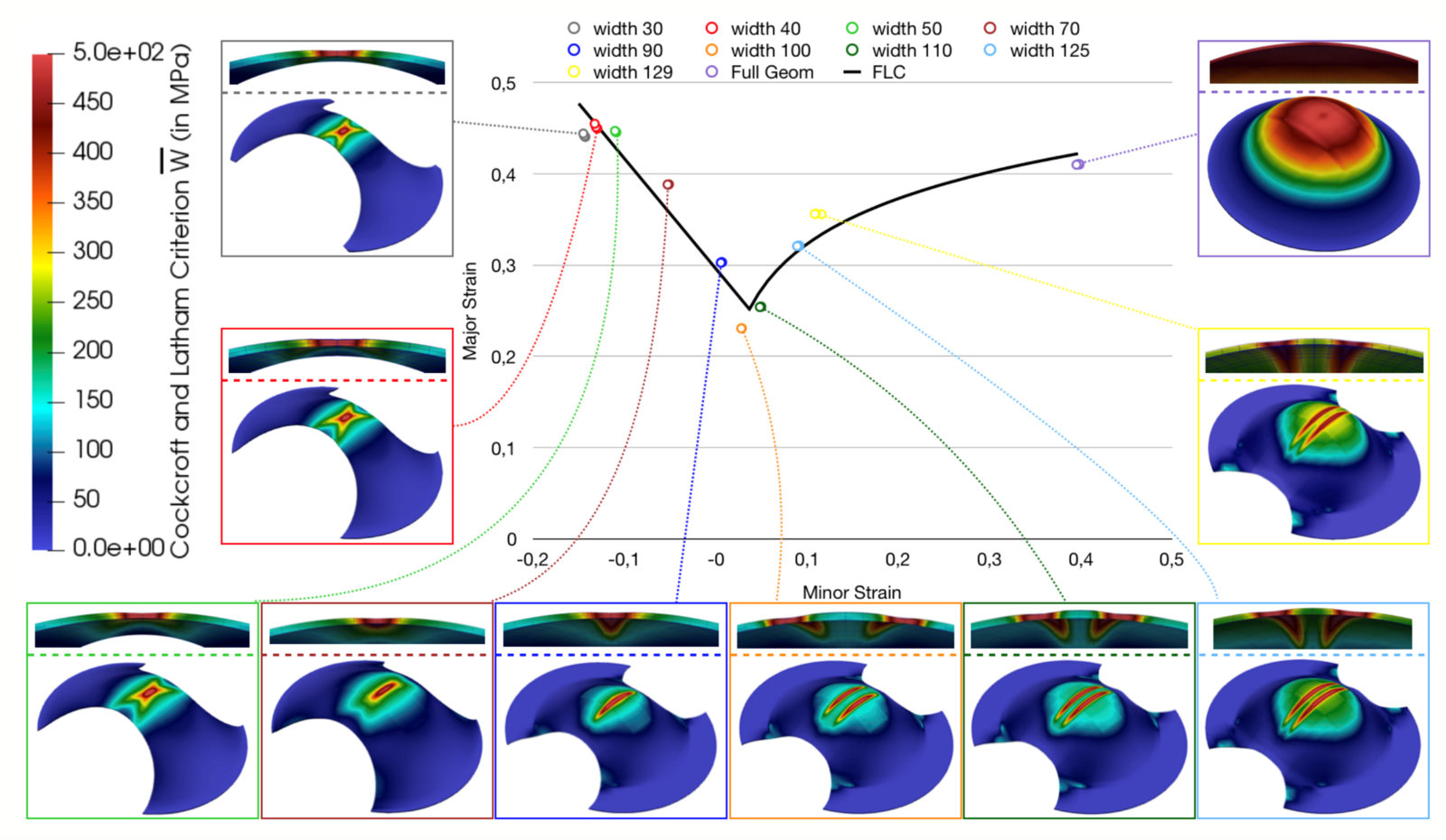
Fig. 4: Virtual FLD computed on JUWELS using the FE2TI software. The computation of the FLD took about 216 hours on 10-15k MPI ranks of the JUWELS supercomputer; figure taken from [5].
References
[1] A. Klawonn, M. Lanser, O. Rheinbach, M. Uran, “Fully-coupled micro-macro finite element simulations of the Nakajima test using parallel computational homogenization”. Comput. Mech. 68 (2021), no. 5, 1153–1178. 74-10
[2] A. Klawonn, S. Köhler, M. Lanser, O. Rheinbach, M. Uran, “Computational homogenization with million-way parallelism using domain decomposition methods”. Comput. Mech. 65 (2020), no. 1, 1–22.
[3] A. Klawonn, M. Lanser, O. Rheinbach, M. Uran, “Nonlinear FETI-DP and BDDC methods: a unified framework and parallel results”. SIAM J. Sci. Comput. 39 (2017), no. 6, C417–C451.
[4] A. Klawonn, M. Lanser, O. Rheinbach, “Oliver Toward extremely scalable nonlinear domain decomposition methods for elliptic partial differential equations”. SIAM J. Sci. Comput. 37 (2015), no. 6, C667–C696.
[5] A. Klawonn, M. Lanser, M. Uran, O. Rheinbach, S. Köhler, J. Schröder, L. Scheunemann, D. Brands, D. Balzani, A. Gandhi, G. Wellein, M. Wittmann, O. Schenk, R. Janalìk, “EXASTEEL - Towards a virtual laboratory for the multiscale simulation of dual-phase steel using high-performance computing”. In: Bungartz HJ., Reiz S., Uekermann B., Neumann P., Nagel W. (eds) Software for Exascale Computing - SPPEXA 2016-2019. Lecture Notes in Computational Science and Engineering, vol 136. Springer, Cham., 2020.