MATERIALS SCIENCE AND CHEMISTRY
Large-scale Phase-Field Simulations of Solid-State Sintering Processes
Principal Investigator:
Dr. Vladimir Ivannikov
Local Project ID:
pn36li
HPC Platform used:
SuperMUC-NG at LRZ
Date published:
Introduction
Sintering is a physically complex process that includes various mechanisms interacting and competing with each other. The obtained densification and microstructure of the sintered packing are of key interest. The accurate prediction of the powder coalescence for a given material and heating profile is a challenging multiphysics problem that couples mass transport and mechanics and involves multiple distinct stages: "early stage" vs. "later stage" (see Fig. 1). These rheological differences justify the application of specialized numerical models and methods with different computational costs for each of the stages.
At Helmholtz-Zentrum Hereon, we conduct experiments and develop numerical tools for simulating sintering processes. These include DEM models [1], which are limited to early-stage simulations but allow to simulate thousands of particles on a simple laptop, and phase- field-based models [2], which are inherently expensive but allow for more accurate predictions. Recent development efforts target the optimizations of our phase-field solver so that tens of thousands of grains can be simulated as in the DEM case. This is necessary to obtain statistically meaningful representative results as well as necessitates the use of supercomputers and the optimization of the code for them.
Figure 1: Visualization of different phases of sintering for a 51-particle packing in 3D.
Results and Methods
Numerics, solution process, and challenges
In the context of phase-field simulations, sintering is described by one Cahn-Hilliard equation and by one Allen-Cahn equation per grain. In practice, non-neighboring grains are merged to order parameters, reducing the number of Allen-Cahn equations needed and the computational costs. The resulting time-dependent non-linear partial differential equations are discretized in space with the finite element method and in time with the backward differentiation formula (BDF2). The nonlinear system is solved with a Newton-Krylov approach, in which we either evaluate exactly the Jacobian or approximate it via finite difference (Jacobian-free Newton-Krylov).
Methods
In order to solve the resulting nonlinear system efficiently, we have proposed different ingredients previously. In the following, we only shortly summarize the most important aspects and refer the interested readers to [3].
We apply matrix-free operator evaluation for fast Jacobian and residual evaluation [4]. Material kernels that are evaluated often have been heavily optimized to use SIMD vectorization and to use well the cache. We have developed block-Jacobi preconditioners that are cheap to set up and to apply, since we apply the same block to multiple grains, allowing to work with multivectors. We proposed a novel distributed grain-tracking and remapping algorithm, which replaces all-to-all communi- cation patterns used in the literature to collect mesh/grain information from all processes. Furthermore, we heavily rely on adaptive mesh refinement, which is crucial to minimize the number of degrees of freedom and concentrate the work at interesting regions (interfaces of grains).
While porting the code to SuperMUC-NG, which allowed us to increase the number of simulated grains from hun- dreds to tens of thousands, we observed non-negligible setup costs, which were related to unfavorable complexities of the algorithm that did not hurt on small scales. We eliminated these and now are able to scale simulations up to 1k nodes. We are in the progress to use these capabilities to quickly run sensitivity studies for different materials, which are investigated by the experimental group at Helmholtz-Zentrum Hereon.
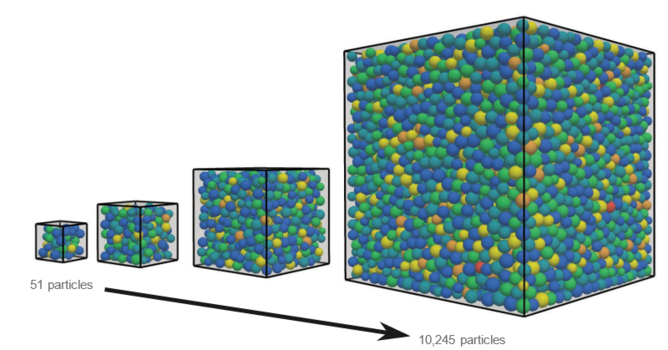
Figure 2: Particle packings considered for the scaling study: 51 - 10,245 particles [3].
Results
Fig. 2 shows some grain packings we considered during our scaling studies. 51 grains (left panel) is a configuration that we mostly consider during code development, since simulations can be quickly run within a few hours on a few nodes of our in-house cluster. 10k grains, on the other hand, is a configuration crucial to obtain statically relevant measurements and requires supercomputing facilities. Fig. 3 indicates that one needs at least 128 nodes for such a configuration due to memory requirements. Furthermore, Fig. 3 contains scaling results of the linear solver for a representative simulation. The timings of the linear solver, which is the most time-consuming part of the nonlinear solution procedure, contain both the evaluation of the Jacobian, which uses the efficient and optimized matrix-free kernels, and the developed block preconditioner. One can observe that, for sufficiently large problem sizes per process, it is possible to increase the number of processes by a factor of 16-32 with only a loss of 25% in parallel efficiency. Furthermore, the lowest times to solution are reached for about 10k DoFs per process, which is in good agreement with the scalability of FEM solvers from other application fields.
Figure 3: Scaling of linear solver for 51 - 10,245 particles [3]. Times are accumulated over 10 time steps
Software
All software developments are available within the open- source project hpsint [5]. It targets HPC systems for sintering applications and is based on deal.II, p4est and Trilinos. The implementation has been verified against results in the literature and shows a clear speedup compared to similar FEM-based solvers.
Ongoing Research/Outlook
Ongoing research adds further physical models that target limitations regarding rigid-body motions and enable liquid-phase sintering relevant in the context of selective laser-melting additive manufacturing processes. Furthermore, we are implementing optimizations regarding data structures, cache locality and preconditioning, which we have identified in [3] and promise a further speedup of 2x.
References
[1] Ivannikov et al. 2021. MSMSE.
[2] Ivannikov et al. 2023. CPM.
[3] Munch et al. 2024. CMS.
[4] Kronbichler, Kormann. 2012. C&F.
[5] github.com/hpsint/hpsint