MATERIALS SCIENCE AND CHEMISTRY
Structure and Dynamics of Polymer and Lipid Systems: Computer Simulation and Numerical Self-consistent Field Theory
Principal Investigator:
Marcus Müller
Affiliation:
Institute for Theoretical Physics, Georg-August University, Göttingen
Local Project ID:
chgu14
HPC Platform used:
JUWELS and JUWELS Booster of JSC
Date published:
Diblock copolymers or biological lipids are comprised of two blocks that thermodynamically repel each other. Since these two blocks are covalently joint into a single molecule, however, they cannot macroscopically phase separated but self-assemble into spatially modulated phases on the scale of the molecule, i.e., 4-100 nm. This self-assembly is a bottom-up strategy for fabricating well-defined, functional nanostructures with applications ranging from semiconductor industries to living cells or synthetic analogs thereof.
In thermodynamic equilibrium the structures are dictated by a balance between the cost of the interfaces between the unlike blocks and the entropy loss of the molecular configurations as the large macromolecules arrange into the nanostructure. In accord with experimental observations, this basic principle predicts similar structures in material systems that significantly differ in their length scales and interactions [1]. For instance, the repulsion between the blocks in synthetic diblock copolymers can be driven by van-der-Waals interactions, whereas the repulsion between hydrophobic tails and hydrophilic heads of the lipids in aqueous solution involves molecular packing and hydrogen bonding. The apparent universality of self-assembly motivates the coarse-grained modeling in our molecular simulations that only capture the relevant interactions for the self-assembly [2]: (i) thermodynamics of the repulsion between the blocks, (ii) molecular connectivity and shape/elasticity of the molecular configurations, and (iii) near-incompressibility of the complex fluid. This use of soft, coarse-grained models dramatically reduces the number of degrees of freedom and increases the smallest time step, associated with an elementary motion, and thereby allows us to access the experimentally relevant large length scales – tens of nanometers (lipids) or micrometer (block copolymers) – long time scales – microseconds (lipid) or hours (block copolymer), as well as large invariant degrees of polymerization.
The typical free-energy difference between competing structures often only amounts to a fraction of the thermal energy scale, kT, per molecule and these complex fluids feature multiple metastable structures, such as e.g., alternate periodic structures, grain boundaries, or local defects [3,4]. This ruggedness of the free-energy landscape implies that self-assembly may be trapped in one of multiple metastable structures and exploring these metastable structures and the kinetic pathways between them is the scientific challenge that we address in our project. Process-directed self-assembly refers to molecular processes that reproducibly trap the self-assembling system into a desired, (meta)stable state [5]. Such thermodynamic processes include inter alia control of global thermodynamic parameters, such as temperature, pressure or membrane tension, as well as localized stimuli such as chemical reactions or the action of membrane proteins that exert local forces.
Example I: Directed self-assembly (DSA) – Using coarse guiding patterns on surfaces, e.g., where only every third stripe domain is prescribed (3×density multiplication), one can direct the kinetics of self-assembly (DSA) into dense, periodic nanostructures that have extremely small defect density and are aligned and registered with the guiding pattern of lines-and-spaces. In the course of structure formation (e.g., after evaporation of a solvent that dilutes the repulsion between the distinct blocks), however, the microphase-separated structure of the block copolymer may become trapped in metastable state, such as e.g., a stitch structure (see Fig. 1) [6].
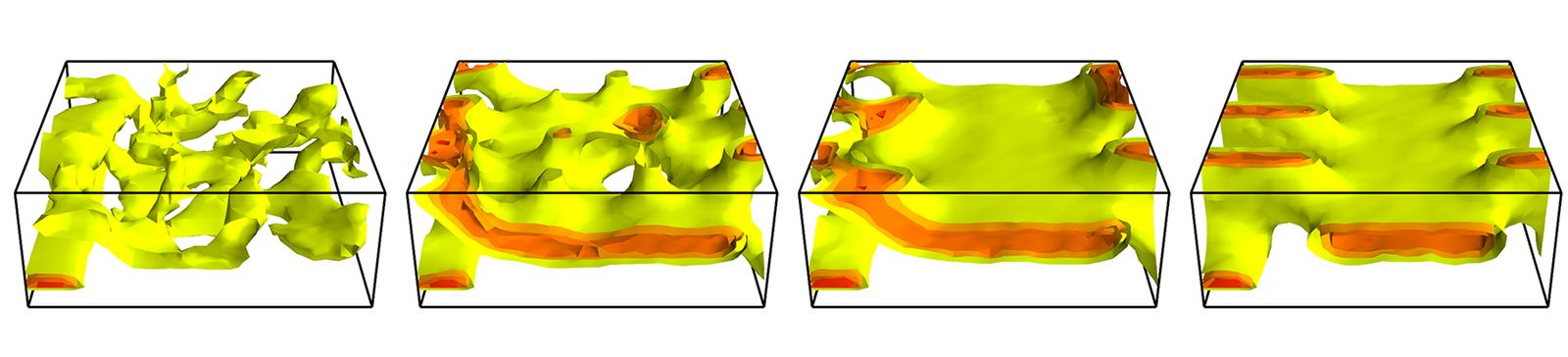
Fig.1: Isocontour plot of the composition of a symmetric diblock copolymer on a guiding pattern (with 3×density multiplication) at various times (t/SMC=1000, 10 000, 100 000, and 499 000 from left to right). The narrow guiding stripe is attractive to one component of the AB diblock, whereas the background substrate is slightly attractive to the other component. The desired equilibrium structure are three vertical stripes. Instead, this metastable, stitch structure forms after a quench from the disordered phase.
For details see J. Rottler and M. Müller, Kinetic pathways of block copolymer directed self-assembly: Insights from efficient continuum modeling, ACS Nano14, 13986 (2020) doi.org/10.1021/acsnano.0c06433
In our particle-based and field-theoretic simulations, we have systematically explored the role of film thickness and interactions of the blocks with the guiding pattern and clarified, under which conditions structures that have no analog in the equilibrium phase diagram form. The simulation reveal (i) that the kinetically accessible structures significantly differ from the equilibrium phases [6], (ii) the importance of accounting of the underlying single-chain dynamics [7], and (iii) the complexity of the structure formation that cannot be simply related to the initial kinetics driven by the guiding pattern [6].
Example II: Membrane fusion – The separation of an inside from an outside lies at the very heart of the organization of living organisms into cells and subcellular compartments. Changes of the topology of biological membranes, such as pore formation, fusion, and fission, are fundamental biophysical processes, involved in a multitude of transport phenomena. Our simulations of the coarse-grained MARTINI model [8] of lipids and proteins study the mechanism of such processes, as quantified by the minimum free-energy path and the concomitant free-energy barriers of transition states [9]. This is a computational challenge because the chemical-potential field of nonequilibrium structures [10] of a molecularly detailed model has to be computed for multiple states along the minimum free-energy path and the path is locally optimized by the string method [11] (see fig. 02). Our simulations demonstrate that lipid architecture, membrane tension, distance and curvature exert a pronounced influence, and they also shed light on the role of fusion/fission proteins [9] that control the distance or local curvature of the apposing membranes [12]. Additionally, the transmembrane parts of fusion and fission proteins locally induce thickness modulations of the membrane that, in turn, facilitate changes of the membrane topology (e.g., pore formation) and induce interactions between protein and fusion/fission intermediates.
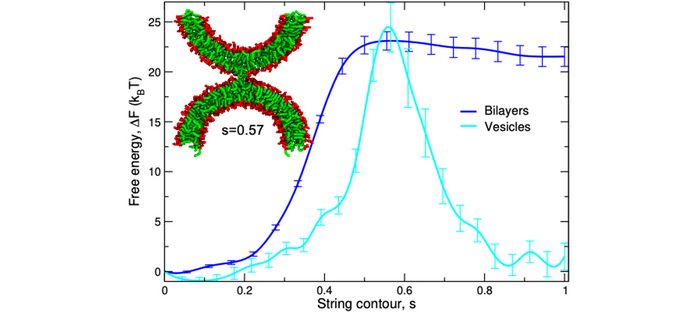
Fig. 2: Free-energy profile along the minimum free-energy path from two apposing bilayers or vesicles (s=0) to a metastable, hydrophobic bridge – the stalk (s=1). The intermembrane distance dw=1.2 nm and 2.3 nm for the planar bilayers and the vesicle, respectively.
Adapted from Y.G. Smirnova and M. Müller, How does curvature affect the free-energy barrier of stalk formation? Small vesicles vs apposing, planar membranes. Eur Biophys J50, 253–264 (2021). https://doi.org/10.1007/s00249-020-01494-1 (CC Attribution 4.0 International License)
Overall, our studies provide insights into the mechanism and free-energy landscapes of structure changes in synthetic or biological self-assembling systems. Using meaningful coarse-grained models and developing new algorithms to accelerate simulations and analyze their outcomes, we mitigate some of the computational costs but supercomputers continue to be essential tools for studying the nonequilibrium processes in these complex, fascinating, and practically relevant fluids.
References
[1] Biological and synthetic membranes: What can be learned from a coarse-grained description? M. Müller, K. Katsov, and M. Schick, Phys. Rep. 434, 113 (2006) https://doi.org/10.1016/j.physrep.2006.08.003
[2] Multi-architecture Monte-Carlo (MC) simulation of soft coarse-grained polymeric materials: SOft coarse grained Monte-carlo Acceleration (SOMA), L. Schneider and M. Müller, Comp. Phys. Comm. 235, 463 (2019) https://doi.org/10.1016/j.cpc.2018.08.011
[3] Kinetics of pattern formation in symmetric diblock copolymer melts, Y.Z. Ren and M. Müller, J. Chem. Phys. 148, 204908 (2018) https://doi.org/10.1063/1.5027741
[4] Directed self-assembly of block copolymers by chemical or topographical guiding patterns: Optimizing molecular architecture, thin-film properties, and kinetics, W.H. Li and M. Müller, Prog. Polym. Sci. 54-55, 47-75 (2016) https://doi.org/10.1016/j.progpolymsci.2015.10.008
[5] Process-directed self-assembly of copolymers: Results of and challenges for simulation studies, M. Müller, Prog. Polym. Sci. 101, 101198 (2020) https://doi.org/10.1016/j.progpolymsci.2019.101198
[6] Kinetic pathways of block copolymer directed self-assembly: Insights from efficient continuum modeling, J. Rottler and M. Müller, ACS Nano 14, 13986 (2020) https://doi.org/10.1021/acsnano.0c06433
[7] Collective short-time dynamics in multicomponent polymer melts, G. Wang, Y. Ren, and M. Müller, Macromolecules 52, 7704 (2019) https://doi.org/10.1021/acs.macromol.9b01709
[8] The Martini force field: coarse grained model for biomolecular simulations, S. Marrink, H.J. Risselada, S. Yefimov, D. Tieleman, A. de Vries A, J Phys Chem B 111, 7812 (2007) https://doi.org/10.1021/jp071097f
[9] Thermodynamically reversible paths of the first fusion intermediate reveal an important role for membrane anchors of fusion proteins, Y.G. Smirnova, H.J. Risselada, and M. Müller, PNAS 116, 2571 (2019) https://doi.org/10.1073/pnas.1818200116
[10] Calculation of membrane bending rigidity using field-theoretic umbrella sampling, Y.G. Smirnova and M. Müller, J. Chem. Phys. 143, 243155 (2015) https://doi.org/10.1063/1.4938383
[11] Transition Path from Two Apposed Membranes to a Stalk Obtained by a Combination of Particle Simulations and String Method, M. Müller, Y.G. Smirnova, G. Marelli, M. Fuhrmans, and A.C. Shi, Phys. Rev. Lett. 108, 228103 (2012) https://doi.org/10.1103/PhysRevLett.108.228103
[12] How does curvature affect the free-energy barrier of stalk formation? Small vesicles vs apposing, planar membranes, Y.G. Smirnova and M. Müller, Eur. Biophys. J. (2021) https://doi.org/10.1007/s00249-020-01494-1
Principle Investigator
Marcus Müller, Institute for Theoretical Physics, Georg-August University, Göttingen, Germany
Project Contributors
Niklas Blagojevic, Marc Fuhrmans, Gregor Ibbeken, Pritam K. Jana, Weihua Li, Louis Pigard, Yongzhi Ren, Juan Carlos Orozco Rey, H. Jelger Risselada, Jörg Rottler (UBC, Canada), Ludwig Schneider, Yuliya Smirnova, Russell Spencer, Dewen Sun, Qiyun Tang, Gaoyuan Wang, Ulrich Welling, Lucia Wesenberg
Scientific Contact
Prof. Dr. Marcus Müller
Georg-August-Universität Göttingen
Institut für Theoretische Physik
Friedrich-Hund-Platz 1, D-37077 Göttingen (Germany)
e-mail: mmueller [@] theorie.physik.uni-goettingen.de
Local project ID: chgu14
August 2021