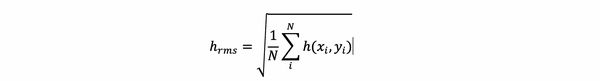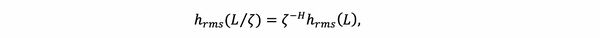The Emergence of Small-scale Self-affine Roughness from Deformation : Gauss Centre for Supercomputing e.V.

Introduction

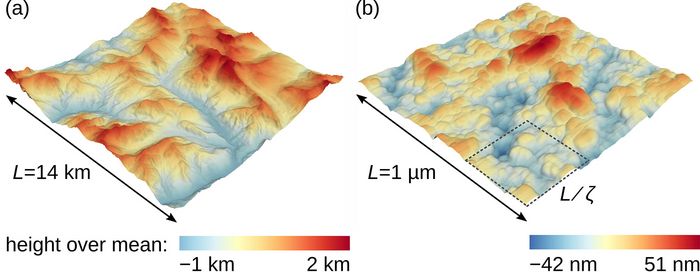
Rough surfaces are everywhere in our environment. While we may perceive some as smooth when we look at them or touch them, there is hardly any natural or artificial surface that is not rough at some scale. The size of features varies drastically, from micrometer-sized asperities and cracks on polished surfaces of household devices, through millimeter scale bumps and pores on construction materials, up to several hundred meters high crags and crevasses in mountain ranges on the surface of the earth, see Fig. 1.

Fig. 1: Topography of (a) a section of the alps [1] (b) a rough metal [2]; the square in (b) has a side length that is a fraction *1/ζ* of the side length L of the whole surface. © IMTEK, University of Freiburg

A remarkable feature is that rough surfaces are often self-affine, meaning that if we zoom in on a part of the surface, we see similar features as on the full surface, but at a different scale [3] [4] [5] [6]. Let h(x,y) be the surface height h at a point described by the coordinates x and y in the plane. A common measure for the roughness of the surface is the root mean square height h_rms. To estimate h_rms , we could measure h(x,y) at N points (x_i,y_i) (i=1…N) and calculate the root mean square of h(x_i,y_i) ,

h_rms may depend on the side length L of the surface, so we write h_rms=h_rms(L) . In the case of a self-affine surface, h_rms scales with L as a power law. Consider a square surface with side length L , e.g. Fig. 1(b). If we zoom in on a square part of the surface with side length L/ζ (where ζ is the level of magnification) and measure h_rms of this part, then we find

where H is a constant independent of ζ . This number is called the Hurst exponent.

Self-affine scaling is observed from the microscopic to the geological scale [7] [8]. How does it emerge? One plausible origin of self-affine roughness is plastic (irreversible) deformation during formation and processing of the body. Necessarily, the surface is deformed, too, and therefore stores the spatial signature of the microscopic mechanisms of deformation. It could then be spatial correlations in these deformation mechanisms which lead to a self-affine topography.

Atomic-scale simulations of surface roughening

One of the goals of project chka18 was to investigate the connection between plastic deformation and roughening. Computer simulations were carried out to determine whether plastic deformation alone could cause self-affine roughening of a body with an initially flat surface. The Molecular Dynamics (MD) simulation technique was used for this purpose. In MD, all atoms in the body are simulated. Quantum mechanical effects are neglected. Instead, the motion of the atoms is assumed to follow classical mechanics, like the motion of Billiard balls. This approximation allows to simulate systems with millions of atoms. Indeed, such a large number of atoms was required to analyze the variation of h_rms(L/ζ) over at least one order of magnitude in ζ .

The starting configurations for MD simulations were cubes with side length of L=100 nm , see Fig. 2. Depending on the material (more on that later), the cubes contained 58 to 83 Mio. atoms. The surfaces along the z -direction were initially atomically flat. Furthermore, periodic boundary conditions were applied in the x - and y -directions (normal to the surface), meaning that atoms with coordinates x≈0 and x≈L , for example, interact with each other. Hence the surfaces of the cube in x - and y -directions do not behave like free surfaces, but like sections in the interior of the body. Effectively, an infinitely wide plate is simulated. The cubes were then compressed simultaneously in x - and y -direction until the side length in these directions had shrunk by 30%.

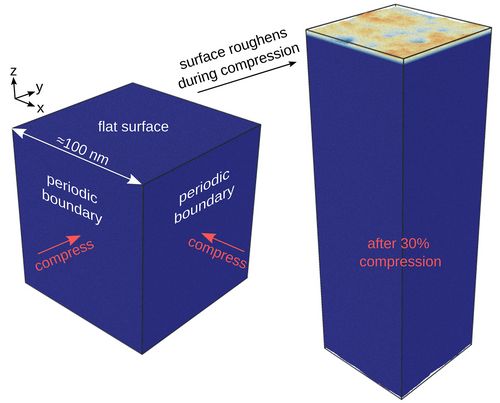
Fig. 2: The initial configuration for MD simulations were cubes with side length of L=100 nm . The cubes had free and initially flat surfaces at the top and at the bottom. The side surfaces were periodic, meaning that atoms on opposite ends interact with each other. The cubes were compressed in two directions, which causes plastic (permanent) deformation, and leads to roughening of the surface (right). © IMTEK, University of Freiburg

Such compression tests were carried out with three different materials: (i) a perfect Gold crystal, where all atoms are arranged on a lattice; (ii) a complex alloy composed of 36.37% Nickel, 36% Cobalt, 16.67% Iron, and 36.67 % Titanium (in percent of the total number of atoms), where the atoms occupy a lattice but the distribution of elements is random; and (iii) a “metallic glass” composed of 50% Copper and Zirconium atoms, respectively, where there is no long-range order of the atoms at all. Fig. 3 illustrates the atomic arrangement in the three materials.

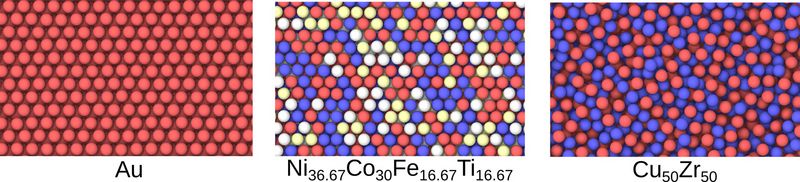
Fig. 3: Illustration of the atomic structure of the materials used in the simulation; colors indicate different elements; pure Gold (left) is initially a perfect crystal, i.e. all atoms are arranged regularly; the alloy Ni_36.67Co₃₀Fe_16.67Ti_16.67 (center) is a crystal as well, but with different elements which are distributed randomly; Cu₅₀Zr₅₀ (right) is a metallic glass, meaning that the atoms are not arranged regularly at all. © IMTEK, University of Freiburg

Fig. 4 shows the topography after 20% compression. The materials roughened to a different degree and different patterns have formed. In the case of the crystals Au and Ni_36.67Co₃₀Fe_16.67Ti_16.67 triangular structures can be identified. They were formed by the intersection of lattice dislocations, which are line-like imperfections in the crystal lattice that cause plastic deformation.

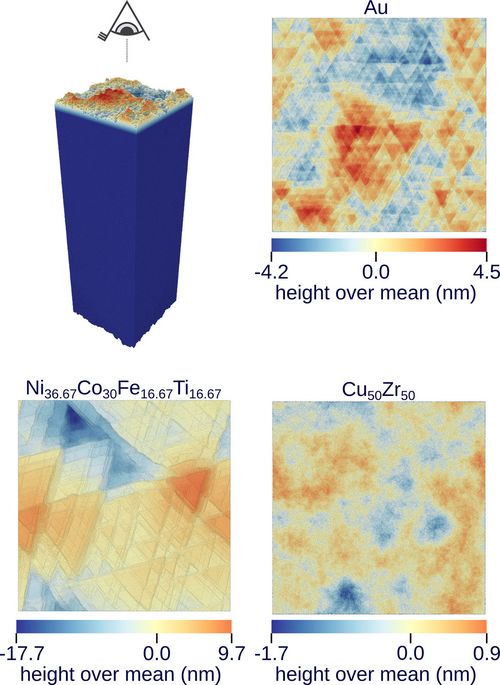
Fig. 4: Birds eye view of the surface after 20% compression. Color indicates the height relative to the mean height of the surface. The three materials have roughened to a different extent. Ni_36.67Co₃₀Fe_16.67Ti_16.67 has the roughest surface, Cu₅₀Zr₅₀ the smoothest. Triangular structures are visible on the surface of the crystals Ni_36.67Co₃₀Fe_16.67Ti_16.67 and Au. These are the traces of lattice dislocations, which enable plastic (permanent) deformation. © IMTEK, University of Freiburg

The scaling of h_rms(L/ζ) with ζ was examined to determine whether the surfaces are self-affine. h_rms(L/ζ) was first calculated for the whole surface (ζ=1 ). Then the surface was subdivided into 4 segments (ζ=2 ), and h_rms was calculated in each sub-segment. This procedure was repeated for higher magnifications ζ=4…128 . In this way, curves of h_rms versus ζ were obtained, and it could be determined that h_rms is indeed self-affine over roughly one order of magnitude in ζ .

A similar scaling analysis was performed for atomic displacements in the interior of the configuration. It was shown that these bulk displacements are self-affine as well. The simulations thus indicate that self-affine roughness may emerge naturally from plastic deformation even on initially flat surfaces. Further details of these simulations, such as the evolution of h_rms with deformation and the effect of temperature, can be found in a recent publication:

Hinkle, A. R., Nöhring, W. G., Leute, R., Junge, T. & Pastewka, L. The emergence of small-scale self-affine surface roughness from deformation. Science Advances 6, eaax0847 (2020) https://doi.org/10.1126/sciadv.aax0847

Who might be interested in these results? The consequences of surface roughness are felt in many ways, even though the connection between a specific effect and the roughness properties of the surface is not always intuitive. For example, surface roughness determines the contact area between surfaces, and therefore surface forces, which in turn affects contact stiffness [10] [11], adhesion [12], and friction [13]. Moreover, roughness affects electrical and thermal transport across interfaces [14] [15]. Besides addressing a topic of general scientific interest, the present study may therefore be useful for other researchers investigating surface-controlled phenomena.

Other project-related publications

Gola, A. & Pastewka, L. Scratching Cu|Au Nanolaminates. Lubricants7, 44(2019). https://doi.org/10.3390/lubricants7050044

Gola, A., Zhang, G.-P., Pastewka, L. & Schwaiger, R. Surface flaws control strain localization in the deformation of Cu|Au nanolaminate pillars. MRS Communications 9, 1067–1071 (2019). https://doi.org/10.1557/mrc.2019.93

Gola, A., Schwaiger, R., Gumbsch, P. & Pastewka, L. Pattern formation during deformation of metallic nanolaminates. Physical Review Materials 4, 013603(2020) https://doi.org/10.1103/PhysRevMaterials.4.013603

References

Topography data from the NASA Shuttle Radar Topography Mission, https://dds.cr.usgs.gov/srtm/version2_1/SRTM3/.
Topography data from T. Jacobs, private communication.
Mandelbrot, B. B. The Fractal Geometry of Nature (W. H. Freeman, 1982).
Sayles, R. S. & Thomas, T. R. Surface topography as a nonstationary random process. Nature 271, 431–434 (1978).
Candela, T., Renard, F., Klinger, Y., Mair, K., Schmittbuhl, J. & Brodsky, E. E. Roughness of fault surfaces over nine decades of length scales. Journal of Geophysical Research: Solid Earth 117, B08409 (2012).
Gujrati, A., Khanal, S. R., Pastewka, L. & Jacobs, T. D. B. Combining TEM, AFM, and profilometry for quantitative topography characterization across all scales. ACS Applied Materials & Interfaces 10, 29169–29178 (2018).
Persson, B. N., Albohr, O., Tartaglino, U., Volokitin, A. I. & Tosatti, E. On the nature of surface roughness with application to contact mechanics, sealing, rubber friction and adhesion. Journal of Physics: Condensed Matter 17 (2005).
Persson, B. N. J. On the Fractal Dimension of Rough Surfaces. Tribology Letters 54, 99–106 (2014).
Hinkle, A. R., Nöhring, W. G., Leute, R., Junge, T. & Pastewka, L. The emergence of small-scale self-affine surface roughness from deformation. Science Advances 6, eaax0847 (2020).
Akarapu, S., Sharp, T. & Robbins, M. O. Stiffness of contacts between rough surfaces. Physical Review Letters 106, 204301 (2011).
Pastewka, L., Prodanov, N., Lorenz, B., Müser, M. H., Robbins, M. O. & Persson, B. N. J. Finite-size scaling in the interfacial stiffness of rough elastic contacts. Physical Review E 87, 062809 (2013).
Pastewka, L. & Robbins, M. O. Contact between rough surfaces and a criterion for macroscopic adhesion. Proceedings of the National Academy of Sciences of the United States of America 111, 3298–3303 (2014).
Bowden, F. P. & Tabor, D. The friction and lubrication of solids (Oxford University Press, 1950).
Binder, L. Der Widerstand von Kontakten. Elektrotechnik und Maschinenbau 30, 781–788 (1912).
Gotsmann, B. & Lantz, M. A. Quantized thermal transport across contacts of rough surfaces. Nature Materials 12, 59–65 (2013).

Research Team

Adam Hinkle^1,2, Wolfram Nöhring², Richard Leute², Till Junge³, Jan Grießer², Adrien Gola⁴

¹ Material, Physical and Chemical Sciences Center, Sandia National Laboratories, Albuquerque, USA
² IMTEK - Department of Microsystems Engineering, University of Freiburg
³ École Polytechnique Fédérale de Lausanne, Switzerland
⁴ Institute for Applied Materials, Karlsruhe Institute of Technology

Scientific Contact

Prof. Dr. Lars Pastewka
IMTEK - Department of Microsystems Engineering
University of Freiburg
Laboratory for Simulation
Georges-Koehler-Allee 103, D-79110 Freiburg (Germany)
e-mail: lars.pastewka [@] imtek.uni-freiburg.de

JSC project ID: chka18

June 2020

MATERIALS SCIENCE AND CHEMISTRY