MATERIALS SCIENCE AND CHEMISTRY
Topological Many-Body Systems with Interactions, Disorder and Periodic Driving
Principal Investigator:
Prof. Dr. Walter Hofstetter
Affiliation:
Goethe-Universität Frankfurt, Institut für Theoretische Physik, Frankfurt, Germany
Local Project ID:
TopoInt
HPC Platform used:
JUWELS Cluster Module and Booster Module of JSC
Date published:
Periodically driven ultracold atomic systems can be used to engineer topologically nontrivial phases, and can give rise to anomalous topological phases with chiral edge modes in the presence of a trivial bulk (AFTI). We have investigated the role of additional quenched disorder and two-particle interactions on this state. Within an exact diagonalization study, we have found signatures of the anomalous Floquet Anderson insulator (AFAI) phase within an experimentally realized model by calculating several indicators [1]. It supports quantized charge pumping through chiral edge states, while the bulk states remain completely localized. Moreover, we have developed an efficient new algorithm for calculating higher-order Chern numbers [2].
We work with a honeycomb lattice system for which AFTI has been realized experimentally [3] and study it in presence of onsite disorder. The system can be modeled by a Hamiltonian, where the details of the periodic driving protocol determine the time-dependent nearest-neighbour hopping matrix elements, which in the absence of driving have the reference value J. In addition, we include an onsite disorder potential which can be experimentally realized by speckle lasers. In our model the disorder has been sampled from a uniform distribution of width W. The periodic driving with frequency Ω allows a description of the system in terms of quasienergy eigenvalues and eigenvectors of a “Floquet Hamiltonian”. The important indicators calculated are the disorder-averaged level-spacing ratio (LSR) of consecutive energy eigenstates, the inverse participation ratio (IPR) measuring the degree of localization of energy eigenfunctions, and the charge pumped (P) from one edge to the other in a cylindrical Laughlin pump setup as a function of a flux threaded through the system.
We find a significant region of the parameter space that shows signatures of the AFAI phase (see Fig. 1). For system sizes ranging from 362 to 802, we find that the bulk states are fully localized for 0.4 ≤ W/Ω ≤ 0.7, while the normalized pumped charge remains quantized to unity (see Fig. 2).
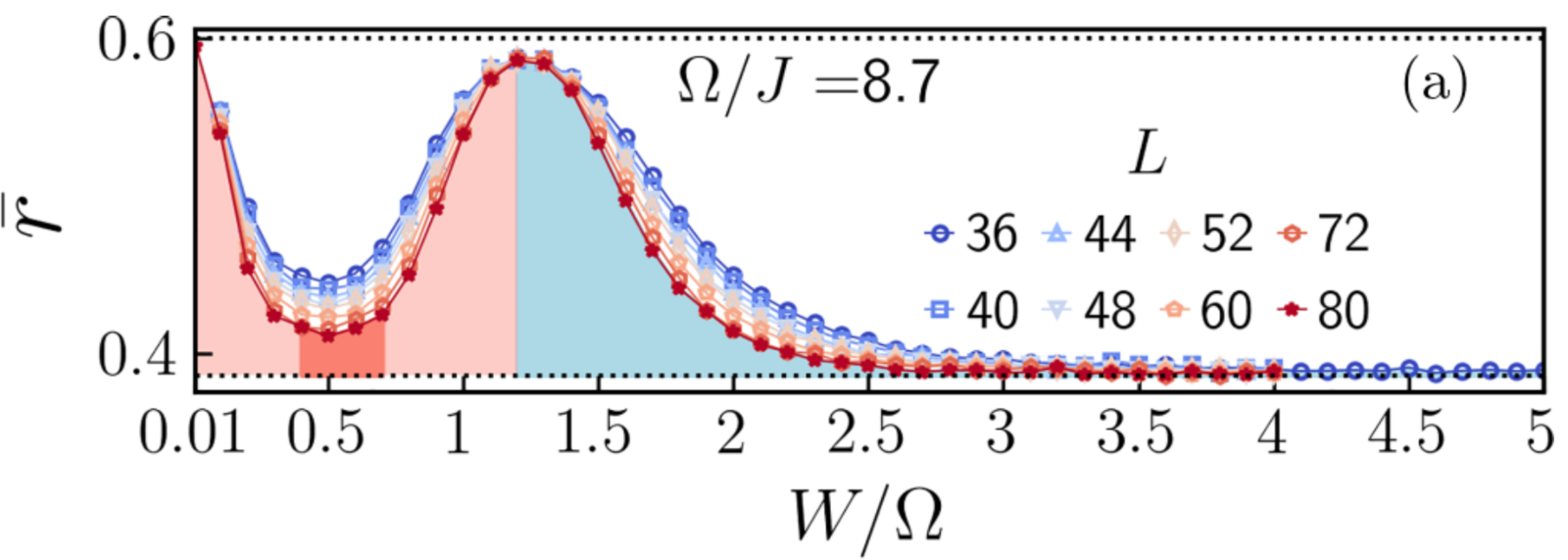
Fig. 1:
Average LSR as a function of W/Ω at Ω/J = 8.7. In the delocalized regime for W/Ω ≤ 0.01 we find a value of approximately 0.6, consistent with the prediction from the Gaussian Unitary Ensemble (GUE) of random matrix theory. In the Anderson-localized regime for W/Ω≥3 we find a value of approximately 0.39, which is consistent with a Poisson distribution of the level spacings. At the maximum at W/Ω ≈ 1.2 the transition from the topological AFAI phase to the trivial Anderson insulator (AI) at stronger disorder occurs. Our finite-size scaling results indicate that the transition from the anomalous localized phase to the AI phase becomes “infinitely sharp” in the thermodynamic limit. Reprinted figure from [1]. Copyright 2024 by the American Physical Society.
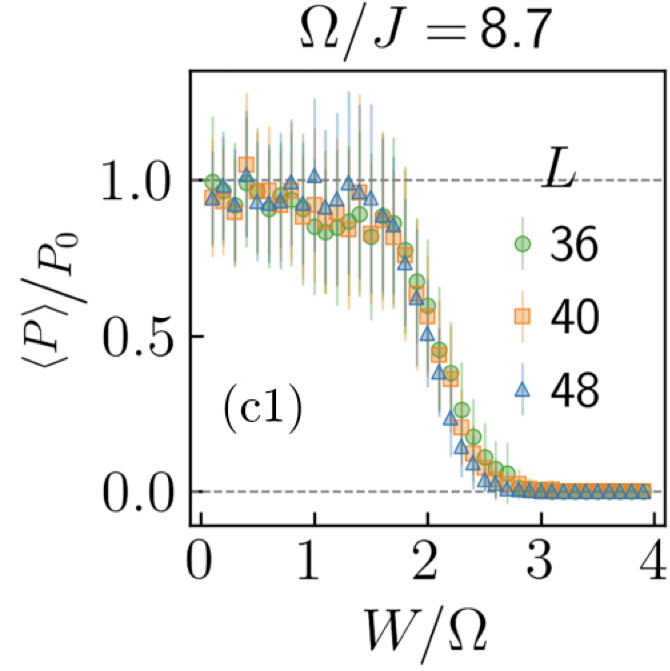
Fig. 2:
Disorder-normalized average pumped charge ⟨P⟩/P0, shown as a function of disorder strength W/Ω for Ω/J = 8.7. It remains quantized to the value 1 (within error bars) for 0.1 ≤ W/Ω ≲ 1.2, corresponding to the anomalous phase. Reprinted figure from [1]. Copyright 2024 by the American Physical Society.
We have also investigated the effect of two-particle interactions on the AFTI phase mentioned above. We have considered the periodically driven Falicov-Kimball (FK) model with a local Hubbard interaction between the itinerant and the immobile fermionic species. Using an implementation of Floquet dynamical mean-field theory [4] we have calculated the single-particle spectral function and the pumped charge. We have found that the AFTI phase is unstable with respect to two-body interactions of the FK-type.
Furthermore, motivated by studies of fermionic systems on quasicrystalline lattices, we have developed a novel, efficient algorithm [2] for calculating the second Chern number C2, which is the topological invariant characterizing the four-dimensional generalization of the quantum Hall effect. Our results show that our algorithm always outperforms the previously established one [5] in both precision and speed.
Our findings will guide experimentalists towards realizing novel exotic topological phases with ultracold atoms. They will also help theorists to determine more efficiently the topological properties of fermionic many-body systems in higher spatial dimensions and in discrete geometries such as quasicrystalline lattices.
References and Publications
[1] A. Dutta, E. Sen, J.-H. Zheng, M. Aidelsburger, and W. Hofstetter, The anomalous Floquet Anderson insulator in a continuously driven optical lattice, Phys. Rev. B 109, L121114 (2024), doi.org/10.1103/PhysRevB.109.L121114
[2] Youjiang Xu, Walter Hofstetter, Getting topological invariants from snapshots: a protocol for defining and calculating topological invariants of systems with discrete parameter space, Preprint arXiv:2311.11618, doi.org/10.48550/arXiv.2311.11618
[3] K. Wintersperger, C. Braun, F.N. Ünal, A. Eckardt, M. Di Liberto, N. Goldman, I. Bloch and M. Aidelsburger, Realization of an anomalous Floquet topological system with ultracold atoms, Nat. Phys. 16, 1058 (2020).
[4] T. Qin, A. Schnell, K. Sengstock, C. Weitenberg, A. Eckardt, and W. Hofstetter, Charge density wave and charge pump of interacting fermions in circularly shaken hexagonal optical lattices, Phys. Rev. A 98, 033601 (2018).
[5] M. Mochol-Grzelak, A. Dauphin, A. Celi, and M. Lewenstein, Efficient algorithm to compute the second Chern number in four dimensional systems, Quan. Sci. Tech. 4, 014009 (2018).