MATERIALS SCIENCE AND CHEMISTRY
Variational Approach to Quantum Many-Body Systems Based on Neural Networks
Principal Investigator:
Prof. Dr. Martin Gärttner
Affiliation:
IFTO, Friedrich-Schiller-University Jena, Germany
Local Project ID:
neuralqmb
HPC Platform used:
JUWELS BOOSTER of JSC
Date published:
The exponential scaling in computational cost when simulating quantum many-body systems poses a significant challenge to their understanding. Variational methods, that approximate the state of the quantum system using an ansatz function, promise to lower that computational cost while making no approximations about the interactions that occur in the system. A novel type of ansatz function, which we explore thoroughly in this project, uses neural networks to approximate the state of the system. As is usual in deep learning, we rely heavily on the use of GPUs during execution, thereby making the use of the JUWELS Booster Module a necessity.
One of the simplest quantum systems is a single spin-1/2. It describes an internal degree of freedom of an elementary particle, such as an electron or a non-elementary particle such as the core of an atom. If the positions of the system constituents of a system of interest are fixed, such as in a two-dimensional lattice for example, the only remaining degree of freedom is the spin of each particle on each lattice site. In our considerations, the particles on the lattice sites are atoms. The spin degree of freedom of each atom is intimately linked with the concept of magnetism; for our considerations here, it will be sufficient to know that each spin gives rise to a magnetic field and at the same time feels the magnetic field at the position where it is located. Thus, the spins on the lattice will interact with each other, giving rise to so-called “collective behavior”, where, for example, all spins may align along one common direction, thereby giving rise to a measurable magnetization.
Simulating this behavior is highly challenging for the following reason. While each single spin-1/2 is described by two complex numbers, a system of N spins requires storing 2N complex numbers – one for each possible state. This makes the simulation of large systems impossible. Already at around 270 atoms, the number of states (each with their own complex number assigned to them) surpasses the number of atoms in the universe. This is what is known as the ‘curse of dimensionality’.
Finding ways to nevertheless gain insights about quantum many-body systems is thus a challenging but highly important endeavor. One option consists in defining ansatz functions, that are described by a fixed number of parameters. Such an ansatz function may be prompted with any one of the 2N configurations, for which it will compute the associated complex number. Importantly, the 2N numbers are never computed nor stored in their entirety. We can learn almost everything about the system of interest by evaluating a fixed number of configurations from the exponentially many. However, we cannot represent all quantum states, since we restrict the number of parameters of the ansatz function. The price we pay for this restriction is thus the expressivity of our ansatz function, meaning the family of states that we can faithfully represent given a certain ansatz function. In our considerations, these ansatz functions are defined by a specific neural network. Learning about the possibilities and the limitations of this neural network inspired approach, is the underlying motivation for this project.
Training and evaluating the performance of deep neural network architectures is a computationally intense task. Thus the use of a GPU cluster was required. We were fortunate that our application for computation time at the JUWELS Booster Module was successful, enabling us to carry out our research without being impeded by maintaining required packages and similar DevOps problems – The JUWELS Booster Team was tremendously helpful in ensuring a swift transition to the new computation environment.
We carried out various projects using the setup described above. We established a new method to simulate the dynamics of open quantum systems, that are in contact with an environment and are thus subject to dissipation. We extended the range of applications to the topic of partial differential equations, that describe the dynamics of continuous probability densities. Finally, we studied which design choices should be in the focus, when constructing neural networks for the laid out applications. These works thus significantly advance our understanding of neural network ansatz functions for describing many-body quantum systems.
Furthermore, we used the available resources to study machine learning approaches to quantum many-body problems that are concerned with their readout, as well as a project aimed at understanding the entropic dynamics in a system of ultracold atoms. A list of the associated publications can be found below.
Publications:
- Tobias Schmale, Moritz Reh and Martin Gärttner: Scalable quantum state tomography with artificial neural networks, npj Quantum Information 8, 115 (2022)
- Moritz Reh, Markus Schmitt and Martin Gärttner: Time-Dependent Variational Principle for Open Quantum Systems with Artificial Neural Networks, Phys. Rev. Lett. 127, 230501 (2021)
- Moritz Reh and Martin Gärttner: Variational Monte Carlo Approach to Partial Differential Equations with Neural Networks, Mach. Learn.: Sci. Technol. 3, 4 (2022)
- Moritz Reh, Markus Schmitt and Martin Gärttner: Optimizing Design Choices for Neural Quantum States, Phys. Rev. B 107, 195115 (2023)
- Maximilian Rieger, Moritz Reh and Martin Gärttner: Sample-efficient estimation of entanglement entropy through supervised learning, Phys. Rev. A 109, 012403 (2024)
- Yannick Deller, Martin Gärttner, Tobi Haas, Markus K. Oberthaler, Moritz Reh, Helmut Strobel: Area laws and thermalization from classical entropies in a spin-1 Bose-Einstein condensate, arXiv:2404.12323
- Yannick Deller, Martin Gärttner, Tobi Haas, Markus K. Oberthaler, Moritz Reh, Helmut Strobel: Area laws and thermalization from classical entropies in a Bose-Einstein condensate, arXiv:2404:12321
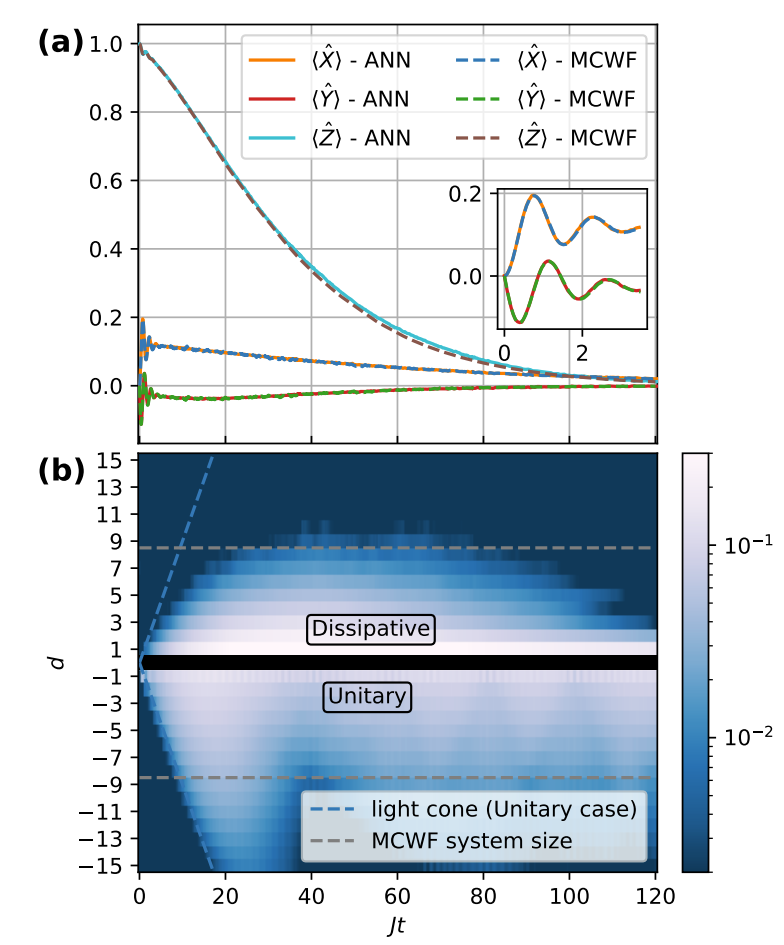
Spin dynamics in an interacting spin chain subject to dissipation. We compare our variational method (ANN) to a method that I exact up to statistical fluctuations (MCWF). (a) Time evolution of components of the magnetization vector. (b) Correlation spreading comparing the evolution with and without dissipation.