ASTROPHYSICS

Introduction

The envelopes of stars such as the Sun are convectively unstable such that fluid motions transport the energy in these regions. These motions are highly turbulent by virtue of the relatively low viscosity and the immense spatial scales involved. The stellar matter is also electrically conductive. In addition, most stars rotate and the fluid is strongly density stratified. For example, in the Sun the pressure scale height increases from 100 km near the surface to about 50,000 km at the base of the convection zone at 0.7 solar radius. The combination of turbulence, rotation, and stratification are conducive to dynamo action, such that fluid motions maintain dynamically important magnetic fields.

Recent observational and numerical results suggest that the convective velocities in simulations are consistently larger than those in the Sun. This has been found from comparisons of simulation data to helioseismic results which rely on the imprints of interior flows on sound waves in the Sun. Furthermore, global simulations with solar luminosity and rotation rate typically produce large-scale differential rotation where the equatorial regions rotate slower than the poles or so-called anti-solar differential rotation. This is opposite to what is observed in the Sun where the equator rotates faster than the poles (solar-like differential rotation). The sense of the differential rotation depends on the rotational influence on the flow which is measured by the ratio of convective turnover time and rotation period or the Rossby number. Anti-solar (solar-like) differential rotation is expected for Rossby number roughly greater (smaller) than unity. The Sun is relatively close to this transition but simulations consistently land on the antisolar regime, indicative of too fast convective flows.

In the current project a new dynamical recipe for radiative diffusion using Kramers opacity law was used. The Kramers opacity law leads to a smooth transition between convective and radiative layers and practically always produces an intermediate layer (Deardorff zone), where the stratification is convectively stable according to the Schwarzschild criterion but still convective with a positive convective energy flux. In such layers, a non-local non-gradient contribution, discovered by James Deardorff in the 1960s, is dominant in the convective transport. The main goal of the project was to study the effects of Kramers opacity law on the properties of convective overshooting, differential rotation, and dynamos in simulations of stellar convection.

Results and Methods

Fully compressible Cartesian and spherical wedge simulations of stellar convection were made with the Pencil Code [1]. The Pencil Code is a high-order finite-difference code written in Fortran 95/2003 for solving ordinary and partial differential equations. The code is parallelized with MPI and domain decomposition. The main application area of the code is astrophysical magnetohydrodynamics (MHD) but it has been used in a wide variety of physics applications such as turbulent combustion, planet formation, and gravitational waves.

The hydrodynamic Cartesian simulations [2] consisted of a convectively unstable layer on top of a stably stratified radiative layer. The main target was to study the dependence of convective overshooting on the energy flux (luminosity) of the star. Using a realistic luminosity in fully compressible simulations of deep stellar convection is infeasible due to the prohibitively long thermal equilibration timescale. Instead, a range of higher normalized fluxes F_n were probed. Such simulations yield a powerlaw dependence for the normalized overshooting depth d_os/H_p, where H_p is the pressure scale height. For the most realistic cases with Kramers’ opacity, d_os is proportional to F_n^0.08 (black, gray, and blue lines in Figure 2). This is much shallower than earlier numerical estimates (~ F_n^0.3). Extrapolating to the solar luminosity (F_n ≈ 10^-11) suggests an overshooting depth of the order of 0.1 H_p or about 5,000km. Furthermore, the difference to the earlier studies can be explained by a difference in the Prandtl number regimes in the respective studies. In the simulations in [2], up to 40% of the convectively mixed layer was formally stably stratified (Deardorff and overshoot zones). The bulk of the simulations in [2] used a modest resolution of 288³ grid points with 288 cores. However, due to the long thermal saturation timescales, several simulations required up to two months wallclock time.

Furthermore, of the order of a hundred low resolution (288³) simulations were made along with subsets a number of runs at 576³ (576 cores) and 1,152³ grid points (2,304 cores) to verify the validity of the low resolution models.

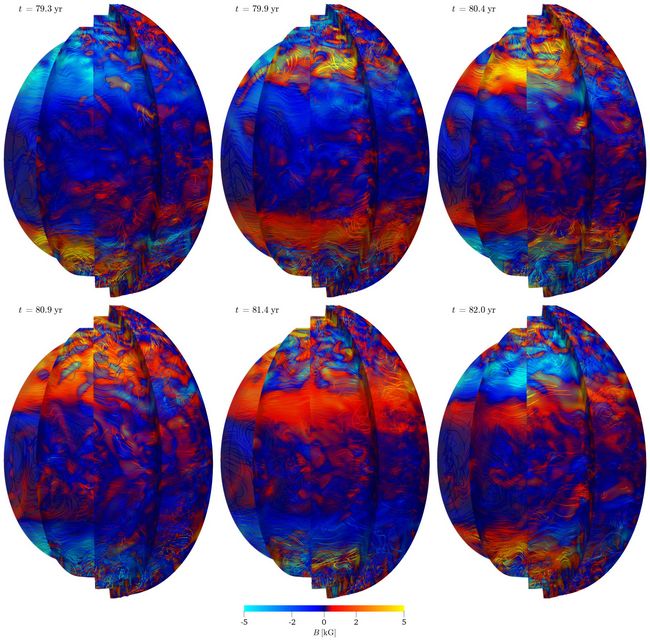
Spherical wedge simulations (Figure 3) were used to probe the effects of Kramers opacity in a more realistic geometry [3,4]. These were the first (semi-) global simulations where the dynamically adapting Kramers opacity is used. The main result of [3] was that although the simulations developed a Deardorff layer, it was much thinner than in the Cartesian cases which is due to the strong rotation and less supercritical convection in the spherical cases. Furthermore, the issue regarding the convective velocity amplitudes is essentially unaffected in these simulations. That is, to achieve a solar-like rotation profile, the rotation rate of the star has to be at roughly twice the actual solar rotation rate. The MHD cases lead to selfconsistent dynamo action and large-scale magnetic fields. Solar-like cyclic dynamo solutions, where the large-scale magnetic fields migrate from mid-latitudes toward the equator in the course of the cycle, are achieved in a narrow parameter regime (Figure 4). However, the magnetic cycle period in these simulations is roughly 3.5 years instead of 22 years as in the Sun.